
【题目】如图,数轴上![]() ,
,![]() 两点对应的有理数分别为
两点对应的有理数分别为![]() 和12,点
和12,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿数轴负方向运动,点
出发,以每秒1个单位长度的速度沿数轴负方向运动,点![]() 同时从点
同时从点![]() 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)求经过2秒后,数轴点![]() 、
、![]() 分别表示的数;
分别表示的数;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在运动过程中是否存在时间![]() 使
使![]() ,若存在,请求出此时
,若存在,请求出此时![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() 表示
表示![]() ,
,![]() 表示4;(2)
表示4;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)根据点P,Q的运动速度及方向可找出t秒时点P,Q表示的数,再代入t=2即可得出结论;
(2)代入t=3可找出点P,Q表示的数,再利用两点间的距离公式可求出PQ的值;
(3)由点A,B表示的数了找出AP,BQ的值,结合AP=BQ可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵点P从点O出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,
∴运动时间为t秒时,点P表示的数为-t,点Q表示的数为2t,
∴当t=2时,点P表示的数为-2,点Q表示的数为4.
(2)当t=3时,点P表示的数为-3,点Q表示的数为6,
∴PQ=6-(-3)=9.
(3)∵点A表示的数为-8,点B表示的数为12,
∴AP=|-t-(-8)|=|8-t|,BQ=|2t-12|.
∵AP=BQ,
∴|8-t|=|2t-12|,
即8-t=2t-12或t-8=2t-12,
解得:![]() 或t=4,
或t=4,
∴当AP=BQ时,t的值为![]() 秒或4秒.
秒或4秒.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
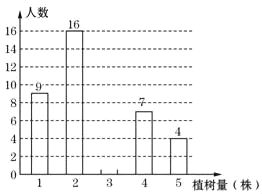
【题目】为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
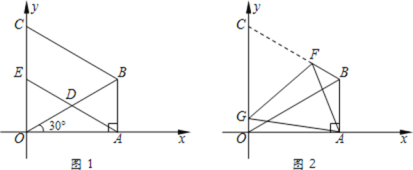
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
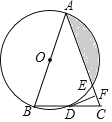
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
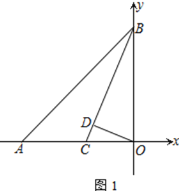
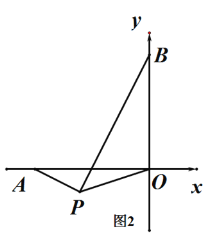
【题目】如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
(1) 求证:BC平分∠ABO
(2) 求![]() 的值
的值
(3) 若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
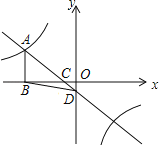
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
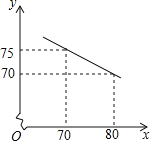
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com