
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.
∵AB⊥BC,∴∠B=90°.
∵AD∥BC,∴∠A=180°﹣∠B=90°,∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得:x=![]() ;
;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得:x=2或x=6,∴满足条件的点P的个数是3个.
故选C.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有![]()
![]()
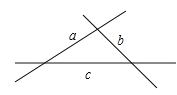
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
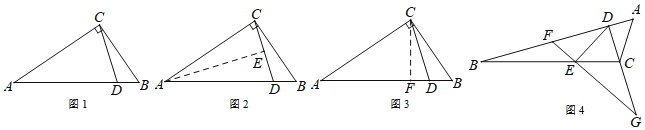
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分成四类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
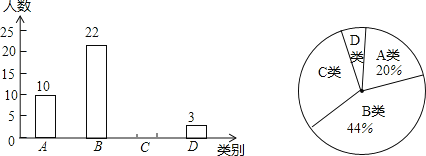
(1)求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数;
(2)若该校九年级男生有500名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
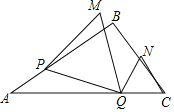
【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=![]() .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=![]() S△QCN时,求t的值;
S△QCN时,求t的值;
(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的有理数分别为
两点对应的有理数分别为![]() 和12,点
和12,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿数轴负方向运动,点
出发,以每秒1个单位长度的速度沿数轴负方向运动,点![]() 同时从点
同时从点![]() 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)求经过2秒后,数轴点![]() 、
、![]() 分别表示的数;
分别表示的数;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在运动过程中是否存在时间![]() 使
使![]() ,若存在,请求出此时
,若存在,请求出此时![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A=50°,则∠D= ;
(2)若∠A=80°,则∠D= ;
(3)若∠A=130°,则∠D= ;
(4)若∠D=36°,则∠A= ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
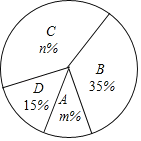
【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩(s) | 频数(人数) |
A | 90<s≤100 | 4 |
B | 80<s≤90 | x |
C | 70<s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com