
【题目】如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A=50°,则∠D= ;
(2)若∠A=80°,则∠D= ;
(3)若∠A=130°,则∠D= ;
(4)若∠D=36°,则∠A= ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.

【答案】(1)25°;(2)40°;(3)65°;(4)72°;(5)∠D=![]() ∠A;
∠A;
【解析】
先根据角平分线定义得到∠ACE=2∠2,∠ABC=2∠1,再根据三角形外角性质得∠ACE=∠ABC+∠A,则2∠2=2∠1+∠A,接着再根据三角形外角性质得∠2=∠1+∠D,易得∠A=2∠D,即∠D=![]() ∠A,然后利用此结论分别解决(1)、(2)、(3)、(4)、(5).
∠A,然后利用此结论分别解决(1)、(2)、(3)、(4)、(5).
解:如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,
∵∠ACE=∠ABC+∠A,
∴2∠2=2∠1+∠A,
而∠2=∠1+∠D,
∴2∠2=2∠1+2∠D,
∴∠A=2∠D,
即∠D=![]() ∠A,
∠A,
(1)当若∠A=50°,则∠D=25°;
(2)若∠A=80°,则∠D=40°;
(3)若∠A=130°,则∠D=65°.
(4)若∠D=36°,则∠A=72°,
(5)综上所述,∠D=![]() ∠A;
∠A;


科目:初中数学 来源: 题型:
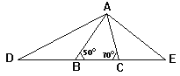
【题目】如图,若△ABC的∠ABC=50°,∠ACB=70°,延长CB至点D,使BD=BA,延长BC至E点,使CE=CA, 连接AD、AE,则∠DAE的度数为__________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
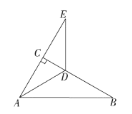
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,试说明DA=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
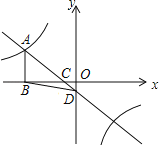
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
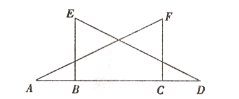
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
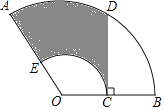
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com