【题目】如图，扇形OAB中，∠AOB=100°，OA=12，C是OB的中点，CD⊥OB交
于点D，以OC为半径的
交OA于点E，则图中阴影部分的面积是（ ）
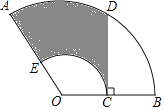
A. 12π+18
B. 12π+36 C. 6π+18 D. 6π+36
亮点激活精编提优100分大试卷系列答案科目：初中数学 来源： 题型：
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩m（单位：分）分成四类：A类（45＜m≤50），B类（40＜m≤45），C类（35＜m≤40），D类（m≤35）绘制出如图所示的两幅不完整的统计图，请根据图中信息解答下列问题：
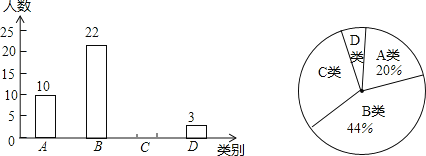
（1）求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数；
（2）若该校九年级男生有500名，D类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知BD是△ABC的角平分线，CD是△ABC的外角∠ACE的外角平分线，CD与BD交于点D．
（1）若∠A=50°，则∠D= ；
（2）若∠A=80°，则∠D= ；
（3）若∠A=130°，则∠D= ；
（4）若∠D=36°，则∠A= ；
（5）综上所述，你会得到什么结论？证明你的结论的准确性．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+4x+c（a≠0）经过点A（﹣1，0），点E（4，5），与y轴交于点B，连接AB．
（1）求该抛物线的解析式；
（2）将△ABO绕点O旋转，点B的对应点为点F．
①当点F落在直线AE上时，求点F的坐标和△ABF的面积；
②当点F到直线AE的距离为
时，过点F作直线AE的平行线与抛物线相交，请直接写出交点的坐标．
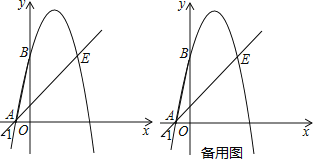
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆货车从百货大楼出发负责送货，向东走了2千米到达小明家，继续向东走了4千米到达小红家，然后向西走了9千米到达小刚家，最后返回百货大楼．
（1）以百货大楼为原点，向东为正方向，1个单位长度表示1千米，请你在数轴上标出小明、小红、小刚家的位置；
（2）小明家与小刚家相距多远？
（3）若货车每千米耗油0.5升，那么这辆货车共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1＋∠4﹦180°,∠2﹦∠E，则EF∥BC，下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容．
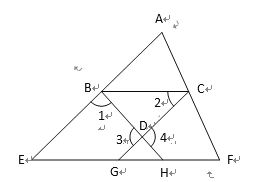
证明：
∵∠1＋∠4﹦180°（ ），
∠3﹦∠4 （ ），
∴∠1﹢ ﹦180°．
∴AE∥CG （ ）
∴∠E﹦∠CGF（ ）．
∵∠2﹦∠E（已知）
∴ ∠2﹦∠CGF（ ）．
∴ BC∥EF（ ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
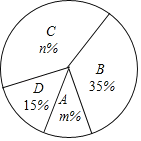
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知多项式（x2+mx﹣
y+3）﹣（3x﹣2y+1﹣nx2）．
（1）若多项式的值与字母x的取值无关，求m，n的值；
（2）先化简多项式3（m2﹣mn﹣n2）﹣（3m2+mn+n2），再求它的值；
（3）在（1）的条件下，求（n+m2）+（2n+
m2）+（3n+
m2）+…+（9n+
m2）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形 ABCD 中，AD∥BC，DC⊥BC，将四边形沿对角线 BD 折叠，点 A 恰好落在 DC 边上的 点 A'处，若∠A'BC=20°，则∠A'BD 的度数为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
