
【题目】已知多项式(x2+mx﹣![]() y+3)﹣(3x﹣2y+1﹣nx2).
y+3)﹣(3x﹣2y+1﹣nx2).
(1)若多项式的值与字母x的取值无关,求m,n的值;
(2)先化简多项式3(m2﹣mn﹣n2)﹣(3m2+mn+n2),再求它的值;
(3)在(1)的条件下,求(n+m2)+(2n+![]() m2)+(3n+
m2)+(3n+![]() m2)+…+(9n+
m2)+…+(9n+![]() m2).
m2).
【答案】(1)m=3,n=﹣1(2)8(3)-28
【解析】
(1)先化简代数式,再根据多项式的值与字母x的取值无关,即可得到含x项的系数等于0,即可得出m,n的值;
(2)化简多项式,再把m=3,n=﹣1代入计算即可;
(3)先运用拆项法化简代数式,再把m=3,n=﹣1代入计算即可得到代数式的值.
解:(1)∵(x2+mx﹣![]() y+3)﹣(3x﹣2y+1﹣nx2)
y+3)﹣(3x﹣2y+1﹣nx2)
=(1+n)x2+(m﹣3)x+![]() y+2,
y+2,
∴当多项式的值与字母x的取值无关时,1+n=0,m﹣3=0,
∴m=3,n=﹣1;
(2)3(m2﹣mn﹣n2)﹣(3m2+mn+n2)
=3m2﹣3mn﹣3n2﹣3m2﹣mn﹣n2
=﹣4mn﹣4n2,
当m=3,n=﹣1时,原式=﹣4×(﹣3)﹣4×1=8;
(3)(n+m2)+(2n+![]() m2)+(3n+
m2)+(3n+![]() m2)+…+(9n+
m2)+…+(9n+![]() m2)
m2)
=n+2n+3n+…+9n+m2+![]() m2+
m2+![]() m2+…+
m2+…+![]() m2
m2
=![]() +m2+m2﹣
+m2+m2﹣![]() m2+
m2+![]() m2﹣
m2﹣![]() m2+…+
m2+…+![]() m2﹣
m2﹣![]() m2
m2
=45n+2m2﹣![]() m2
m2
=45n+![]() m2
m2
当m=3,n=﹣1时,原式=﹣45+![]() ×9=﹣45+17=﹣28.
×9=﹣45+17=﹣28.
故答案为:(1)m=3,n=﹣1;(2)8;(3)-28.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
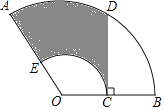
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
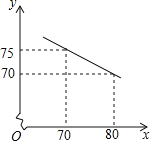
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
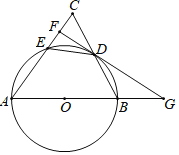
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:FG是⊙O的切线;
(2)若tanC=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s.
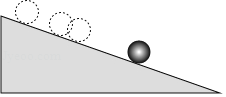
(1)求小球速度v(单位:m/s)关于时间t(单位:s)的函数解析式,它是一次函数吗?
(2)求第3.5s时小球的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮 | 第2轮 | 第3轮 | 第4轮 | 第5轮 | 第6轮 | |
甲 | 10 | 14 | 12 | 18 | 16 | 20 |
乙 | 12 | 11 | 9 | 14 | 22 | 16 |
下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com