
【题目】目前节能灯在城市已基本普及,为满足消费者需求,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、标价如下表:
进价(元/只) | 标价(元/只) | |
甲型 | 25 | 40 |
乙型 | 45 | 60 |
(1)如何进货才能保证进货款恰好为46000元?
(2)由于恰逢五一,商场决定搞促销活动,乙型节能灯打八五折,请你运用所学的知识预算一下甲型节能灯要打几折才能使这批灯售完后获得9200元的利润(不考虑其它因素)?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
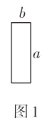
图1是一个长为![]() ,宽为
,宽为![]() 的长方形.现有相同的长方形若干,进行如下操作:
的长方形.现有相同的长方形若干,进行如下操作:
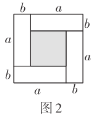
(1)用四块图1的小长方形不重叠地拼成一个如图2所示的正方形.请利用图2中阴影部分面积的不同表示方法,直接写出代数式![]() ,
,![]() ,
,![]() 之间的等量关系___________;
之间的等量关系___________;
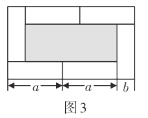
(2)将六块图1的小长方形不重叠地拼成一个如图3所示的长方形,通过不同方法计算阴影部分的面积,你能得到什么等式?请写出你的结论并用乘法法则证明这个等式成立;
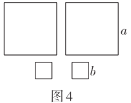
(3)现有图1的小长方形若干个,图4边长为![]() 的正方形两个,边长为
的正方形两个,边长为![]() 的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为
的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为![]() .画出你所拼成的长方形,并写出长方形的长和宽分别为多少.
.画出你所拼成的长方形,并写出长方形的长和宽分别为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
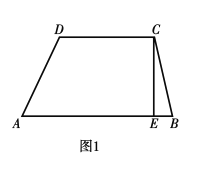
【题目】如图1,梯形![]() 中,上底
中,上底![]() 下底
下底![]() 高
高![]() 梯形的面积
梯形的面积![]() 动点
动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.
![]() 请根据
请根据![]() 与
与![]() 的关系式,完成下列问题:
的关系式,完成下列问题:
|
|
|
|
| ··· | |
|
|
|
| ··· |
![]() 补充表格中的数据;
补充表格中的数据;
![]() 当
当![]() 时,表示的图形是_ .
时,表示的图形是_ .
![]() 梯形的面积
梯形的面积![]() 与
与![]() 的关系如图2所示,则点
的关系如图2所示,则点![]() 表示的实际意义是_ ;
表示的实际意义是_ ;

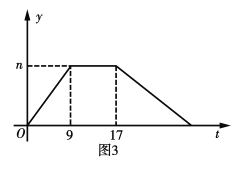
![]() 若点
若点![]() 运动的时间为
运动的时间为![]() 的面积为
的面积为![]() 与
与![]() 的关系如图3所示.求
的关系如图3所示.求![]() 的长和
的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
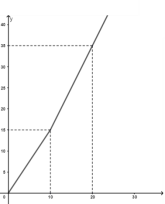
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=90°.
(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(2)如图2,设BC边上的中线为AD,求证:BC=2AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,点G为AD的中点,连接BG并延长,交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高.正确的个数有( )
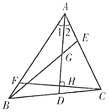
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
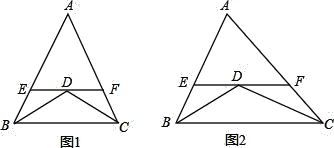
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
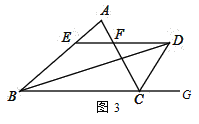
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com