
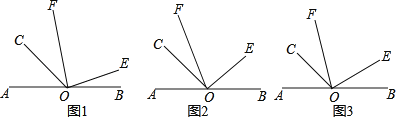
【题目】如图,O是直线AB上的一点,∠AOC=45°,OE是∠BOC内部的一条射线,且OF平分∠AOE.
(1)如图1,若∠COF=35°,求∠EOB的度数;
(2)如图2,若∠EOB=40°,求∠COF的度数;
(3)如图3,∠COF与∠EOB有怎样的数量关系?请说明理由.
【答案】(1)∠EOB=20°;(2)∠COF= 25°;(3)∠EOB+2∠COF=90°,理由见解析.
【解析】
(1)OF平分∠AOE得出∠AOF=∠EOF,再利用∠BOE与∠AOE是邻补角这一关系解答即可;
(2)分析方法如上题,OF平分∠AOE得出∠AOF=∠EOF,再利用∠BOE与∠AOE是邻补角相加等于180°解答即可;
(3)分析方法同上,设∠COF与∠EOB的度数分别是α和β,再计算得出数量关系即可.
(1)∵∠AOC=45°,∠COF=35°
∴∠AOF=∠AOC+∠COF=80°
∵OF平分∠AOE,
∴∠AOE=2∠AOF=160°
∵∠AOB是平角
∴∠AOB=180°
∴∠EOB=∠AOB﹣∠AOE=20°
答:∠EOB的度数是20°.
(2)∠AOE=180°﹣40°=140°
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=70°
∠AOE=70°
∴∠COF=∠AOF﹣∠AOC=70°﹣45°=25°
答:∠COF的度数是25°.
(3)∠EOB+2∠COF=90°,理由如下:
设∠COF=α,∠BOE=β
∵∠AOB是平角,
∴∠AOE=180°﹣β
∵OF平分∠AOE,
∴2∠AOF=∠AOE=180°﹣β
∴2α=2∠COF=2(∠AOF﹣∠AOC )
=2∠AOF﹣2∠AOC
=180°﹣β﹣2×45°=90°﹣β
∴2α+β=90°
即∠EOB+2∠COF=90°.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.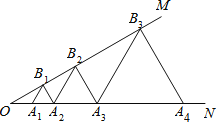
查看答案和解析>>
科目:初中数学 来源: 题型:
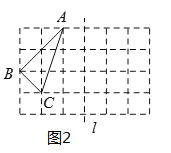
【题目】(1)如图②,利用网格线画![]() ,使它与
,使它与![]() 关于直线
关于直线![]() 对称.若每个小正方形边长为1,则
对称.若每个小正方形边长为1,则![]() 的面积为__.
的面积为__.
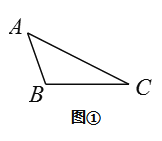
(2)如图①,用直尺和圆规在△ABC的一边![]() 上确定一点
上确定一点![]() ,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
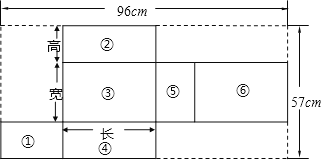
【题目】如图是某涌泉蜜桔长方体包装盒的展开图.具体数据如图所示,且长方体盒子的长是宽的2倍.
(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是 与 , 与 , 与 ;
(2)若设长方体的宽为xcm,则长方体的长为 cm,高为 cm;(用含x的式子表示)
(3)求这种长方体包装盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
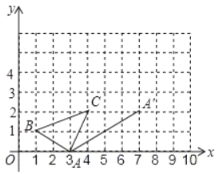
【题目】在直角坐标系中,![]() 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将![]() 沿
沿![]() 的方向平移,使得点
的方向平移,使得点![]() 移至图中的点
移至图中的点![]() 的位置.
的位置.
(1)在直角坐标系中,画出平移后所得![]() (其中
(其中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的对应点).
的对应点).
(2)(1)中所得的点![]() ,
,![]() 的坐标分别是________,________.
的坐标分别是________,________.
(3)直接写出![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A出发以每秒2 cm的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△APQ是以PQ为底边的等腰三角形时,运动的时间是 ( ).
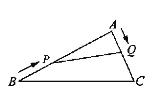
A. 2.5 sB. 3 sC. 3.5 sD. 4 s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com