
����Ŀ������ABC�У���ACB=90��AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E.
(1)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ����֤��DE=AD+BE��
(2)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ�����ʣ�DE��AD��BE�������ĵ�����ϵ����д�����������ϵ��������֤��.
(3)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ��DE��AD��BE֮��ĵ�����ϵ�� (ֱ��д���𰸣�����֤��.)
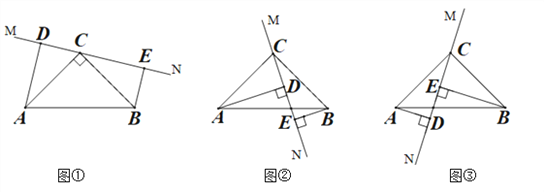
���𰸡���1��֤������������2��AD-BE=DE��֤������������3��BE-AD=DE.
�����������������
��1������֪������֤��DAC�͡�DCA���࣬��ECB�͡�DCA���࣬�ɴ˿ɵá�DAC=��ECB�����������������֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ϳ�֤�ã�DE=DC+CE=AD+BE��
��2���ɣ�1����˼·֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ӷ��ɵã�DE=CE-CD=AD-BE��
��3��ͬ��2����˼·֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ӷ��ɵã�DE=CD-CE=BE-AD.
���������
��1����AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У� 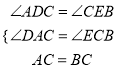 ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=DC+CE��
��DE=AD+BE.
��2����ͼ�ڣ�DE��AD��BE�Ĺ�ϵΪ��DE=AD-BE.�������£�
��AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У�  ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=CE-CD��
��DE=AD-BE.
��3����ͼ����DE��AD��BE֮��ĵ�����ϵ����DE=BE-AD���������£�
��AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У�  ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=CD-CE��
��DE=BE-AD.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������3����0������3��2��|��9|����14�У�������_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() +
+![]()
![]()
![]() ����
����![]()
����![]() ����
���� ![]()
![]()
����![]() ����25��
����25��![]() �D(�D25)��
�D(�D25)��![]() ��25��(��
��25��(��![]() )
)
����![]() ����100
����100![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB��CD��DE��AC��BF��AC��E��F�Ǵ��㣬AE=CF��
��֤��(1)DE=BF��(2)AB��CD��
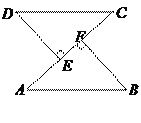
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͬѧ������ѧ���飬�����óɼ����÷�ȡ���������������ֳ����飬�����Ƴ�Ƶ��ֱ��ͼ����ͼ��������ֱ��ͼ�ṩ����Ϣ���ش��������⣺ 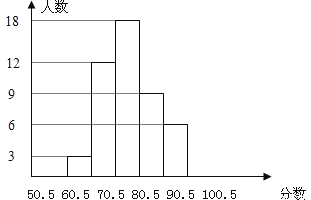
��1���ð�ж�����ѧ���μ���β��飿
��2����60.5��70.5��һ�����ε�Ƶ���Ƕ��٣�
��3����80������Ϊ���㣬��ð���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����2x3my4�멁3x9y2n��ͬ�����ôm��n��ֵ�ֱ�Ϊ�� ��
A.m=��2��n=3
B.m=2��n=3
C.m=��3��n=2
D.m=3��n=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������ؽ�����ijУѧ����������֪��һ�ξ���ܶ�Ϊ9000Ԫ���ڶ��ξ���ܶ�Ϊ12000Ԫ�������˾�������ȣ����ڶ��ξ�������ȵ�һ�ζ�50�ˣ����У�ڶ��ξ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���߶�AB=6cm��C���P�������1cm/s���ٶ���AB�����˶���D���B������2cm/s���ٶ���AB�����˶���C���߶�AP�ϣ�D���߶�BP�ϣ� 
��1����C��D�˶�������ʱ�̶���PD=2AC�����P��AB�ϵ�λ�ã�
��2���ڣ�1���������£�Q��ֱ��AB��һ�㣬��AQ��BQ=PQ����PQ��ֵ��
��3���ڣ�1���������£���C��D�˶���һ��ʱ���ǡ��AB=2CD����ʱ��Cֹͣ�˶�����������߶�PB���˶���M��N�ֱ���CD��PD���е㣬���MN��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com