
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
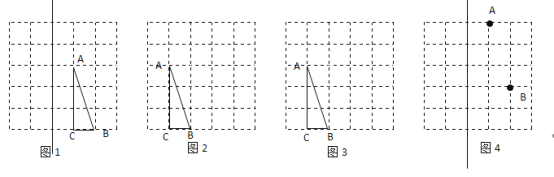
【答案】(1)图见解析;(2)图见解析;(3)图见解析;(4)图见解析
【解析】
(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 即可;
即可;
(2)如解图2,连接CH,交AB于点D,利用SAS证出△ACB≌△CGH,从而得出∠BAC=∠HCG,然后利用等量代换即可求出∠CDB=90°;
(3)如解图3,连接CP交AB于点E,利用矩形的性质可得AE=BE;
(4)如解图4,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM,根据平行四边形的性质和两点之间线段最短即可推出此时MN即为所求.
解:(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
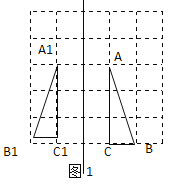
、![]() ,如图1所示,
,如图1所示,![]() 即为所求;
即为所求;
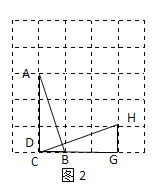
(2)如图2所示连接CH,交AB于点D,
在△ACB和△CGH中
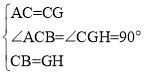
∴△ACB≌△CGH
∴∠BAC=∠HCG
∵∠BAC+∠ABC=90°
∴∠HCG+∠ABC=90°
∴∠CDB=90°
∴CD为△ABC的高,故CD即为所求;
(3)如图3所示,连接CP交AB于点E
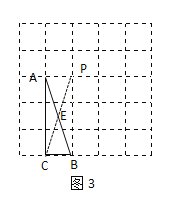
由图可知:四边形ACBP为矩形
∴AE=EB
∴CE为△ABC的中线,故CE即为所求;
(4)如图4所示,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM
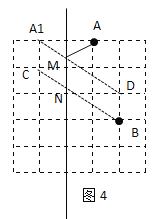
根据对称性可知:AM=A1M
由图可知:A1C=BD=1个单位长度,A1C∥BD∥直线l
∴四边形A1CBD为平行四边形
∴A1D∥BC
∴四边形A1CNM和四边形MNBD均为平行四边形
∴A1M=CN,MN=BD=1个单位长度
∴AM=CN
∴AM+NB=CN+NB=CB,
根据两点之间线段最短,此时AM+NB最小,而MN=1个单位长度为固定值,
∴此时![]() 最小,故此时MN即为所求.
最小,故此时MN即为所求.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
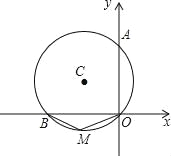
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
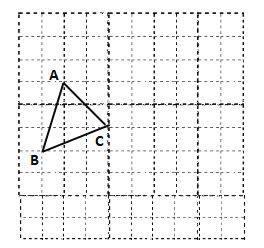
【题目】如图,在边长为1的小正方形组成的10×10网络中(我们把组成网格的小正方形的顶点称为格点),△ABC的三个顶点分别在网格的格点上
(1)请你在所给的网格中建立平面直角坐标系,使△ABC的顶点A的坐标为(-3,5);
(2)在(1)的坐标系中,直接写出△ABC其它两个顶点的坐标;
(3)在(1)的坐标系中,画出△ABC关于y轴对称的图形△A1B1C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣4x+c经过点A(2,0).
(1)求抛物线的解析式和顶点坐标;
(2)若点B(m,n)是抛物线上的一动点,点B关于原点的对称点为C.
①若B、C都在抛物线上,求m的值;
②若点C在第四象限,当AC2的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
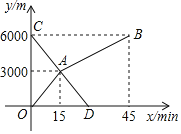
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,然后改为步行,到达图书馆恰好用45min:小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示.
(1)家与图书馆之间的路程为 m,小东从图书馆到家所用的时间为 .
(2)求小玲步行时y与x之间的函数关系式.
(3)求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,∠BAC.求作:∠BAC的角平分线AP.
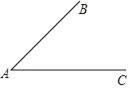
小霞的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
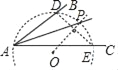
所以射线AP为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com