
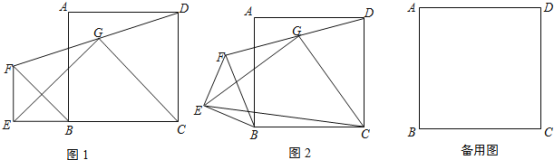
【题目】四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及![]() 的值;
的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,![]() ,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
【答案】(1)EG⊥CG,![]() ;(2)结论还成立,证明见解析;
;(2)结论还成立,证明见解析;
【解析】
试题(1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=![]() (EF+DC)=
(EF+DC)=![]() (EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可.
(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可.
(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案.
(3)连接BD,求出![]() ,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.
,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.
试题解析:(1)EG⊥CG,![]() ,理由是:
,理由是:
如图1,过G作GH⊥EC于H,
∵∠FEB=∠DCB=90°,∴EF∥GH∥DC.
∵G为DF中点,∴H为EC中点.
∴EG=GC,GH=![]() (EF+DC)=
(EF+DC)=![]() (EB+BC),即GH=EH=BC.
(EB+BC),即GH=EH=BC.
∴∠EGC=90°,即△EGC是等腰直角三角形.
∴![]()
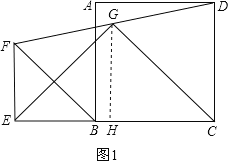
(2)结论还成立,证明如下:
如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,
∵在△EFG和△HDG中,GF=GD,∠FGE=∠DGH,EG=HG,∴△EFG≌△HDG(SAS).
∴DH=EF=BE,∠FEG=∠DHG.∴EF∥DH.
∴∠1=∠2=90°-∠3=∠4.∴∠EBC=180°-∠4=180°-∠1=∠HDC.
在△EBC和△HDC中,BE=DH,∠EBC=∠HDC,BC=CD,∴△EBC≌△HDC.
∴CE=CH,∠BCE=∠DCH.
∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°.
∴△ECH是等腰直角三角形,
∵G为EH的中点,
∴EG⊥GC,![]() ,即(1)中的结论仍然成立.
,即(1)中的结论仍然成立.
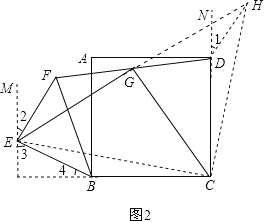
(3)如图3,连接BD,
∵AB=![]() ,正方形ABCD,∴BD=2.∴
,正方形ABCD,∴BD=2.∴![]() .
.
∴∠DBE=60°.∴∠ABE=∠DBE-∠ABD=15°.∴∠ABF=45°-15°=30°.
∴![]() .∴DE=
.∴DE=![]() BE=
BE=![]() .
.
∴DF=DE-EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1,x2是方程的两个实数根,且x12+x22=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
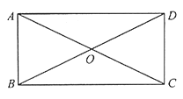
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是两根木棒及其影子的情形.

(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
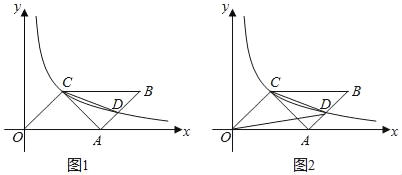
【题目】如图1,在平面直角坐标系中,OABC的一个顶点与坐标原点重合,OA边落在x轴上,且OA=4,OC=2![]() ,∠COA=45°.反比例函数y=
,∠COA=45°.反比例函数y=![]() (k>0,x>0)的图象经过点C,与AB交于点D,连接AC,CD.
(k>0,x>0)的图象经过点C,与AB交于点D,连接AC,CD.
(1)试求反比例函数的解析式;
(2)求证:CD平分∠ACB;
(3)如图2,连接OD,在反比例的函数图象上是否存在一点P,使得S△POC=![]() S△COD?如果存在,请直接写出点P的坐标.如果不存在,请说明理由.
S△COD?如果存在,请直接写出点P的坐标.如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 是反比例函数.
是反比例函数.
(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(![]() ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
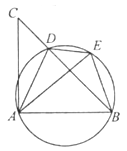
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
材料2.已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2-x-1=0的两个不相等的实数根,
根据材料1得m+n=1,mn=-1,
∴![]() .
.
解决问题:
(1)一元二次方程x2-4x-3=0的两根为x1,x2,则x1+x2= ,x1x2= .
(2)已知实数m,n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
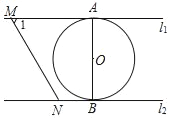
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=![]() ;②若MN与⊙O相切,则AM=
;②若MN与⊙O相切,则AM=![]() ;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com