
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1,x2是方程的两个实数根,且x12+x22=4,求k的值.
【答案】(1)当k≤![]() 时,方程有实数根;(2)k=0.
时,方程有实数根;(2)k=0.
【解析】
(1)要使方程有实数根,必须△≥0,即4(k﹣1)2﹣4k2≥0;(2)由韦达定理得,x1+x2=2(k﹣1),x1x2=k2,故x12+x22=(x1+x2)2﹣2x1x2.
解:(1)要使方程有实数根,必须△≥0
即4(k﹣1)2﹣4k2≥0
解得k≤![]() ,∴当k≤
,∴当k≤![]() 时,方程有实数根.
时,方程有实数根.
(2)由韦达定理得,x1+x2=2(k﹣1),x1x2=k2
∴x12+x22=(x1+x2)2﹣2x1x2
=4(k﹣1)2﹣2k2
=2k2﹣8k+4,
∵x12+x22=4,
∴2k2﹣8k+4=4
解得k1=0,k2=4,
由(1)知k≤![]() ,∴k=4不合题意,
,∴k=4不合题意,
∴k=0.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
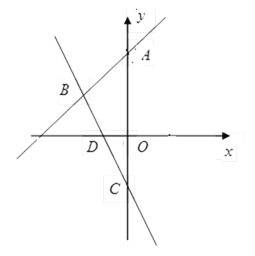
【题目】如图,在平面直角坐标系中,直线AB与直线BC相交于点![]() ,直线AB与
,直线AB与![]() 轴相交于点
轴相交于点![]() ,直线BC与
,直线BC与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点C.
、点C.
(1)求直线AB的解析式;
(2)过点A作BC的平行线交![]() 轴于点E,求点E的坐标;
轴于点E,求点E的坐标;
(3)在(2)的条件下,点P是直线AB上一动点且在![]() 轴的上方,如果以点D、E、P、Q为顶点的平行四边形的面积等于△ABC,请求出点P的坐标,并直接写出点Q的坐标.
轴的上方,如果以点D、E、P、Q为顶点的平行四边形的面积等于△ABC,请求出点P的坐标,并直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
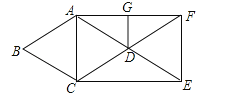
【题目】(3分)如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是![]()
C.四边形ACEF是平行四边形,它的周长是![]()
D.四边形ACEF是矩形,它的周长是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
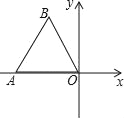
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=110°,∠BOC=a.将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,则△ADC≌△BOC,连接 OD.
(1)求证:△COD 是等边三角形;
(2)当α=120°时,试判断 AD 与 OC 的位置关系,并说明理由;
(3)探究:当 a 为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
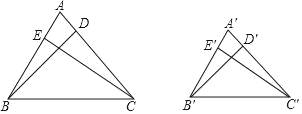
【题目】如图,在△ABC与△A'B'C'中,∠A=∠A',BD、CE是△ABC的高,B'D'、C'E'是△A'B'C'的高,点D、E、D'、E'分别在AC、AB、A'C'、A'B'上,且![]() .
.
求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于![]() ,那么每套售价至少是多少元?
,那么每套售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com