
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=110°,∠BOC=a.将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,则△ADC≌△BOC,连接 OD.
(1)求证:△COD 是等边三角形;
(2)当α=120°时,试判断 AD 与 OC 的位置关系,并说明理由;
(3)探究:当 a 为多少度时,△AOD 是等腰三角形?

【答案】(1)证明见解析;(2)证明见解析;(3)当 a 为 125°或 110°或 140°时,△AOD 是等腰三角形.
【解析】
(1)根据旋转得出CO=CD,∠DCO=60°,根据等边三角形的判定推出即可.
(2)求出∠ADO=∠COD=60°,根据平行线的判定推出即可.
(3)用∠α表示∠ADO、∠AOD、∠DAO,分为三种情况:①∠ADO=∠AOD,②∠ADO=∠OAD,③∠OAD=∠AOD,代入求出即可.
证明:(1)∵△ADC≌△BOC,
∴CO=CD,
∵将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,
∴∠DCO=60°,
∴△COD 是等边三角形.
(2)解:AD∥OC,
理由是:∵△DOC 是等边三角形,
∴∠CDO=∠DOC=60°,
∵∠α=120°,△COB≌△CDA,
∴∠ADC=∠COB=120°,
∴∠ADO=120°﹣60°=60°,
∴∠ADO=∠DOC=60°,
∴AD∥OC.
(3)解:∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣110°﹣∠α﹣60°=190°﹣∠α,∠ADO=∠ADC﹣∠CDO=∠α﹣60°,∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(190°﹣∠α)=50°, 若∠ADO=∠AOD,即∠α﹣60°=190°﹣∠α,
解得:∠α=125°;
若∠ADO=∠OAD,则∠α﹣60°=50°, 解得:∠α=110°;
若∠OAD=∠AOD,即 50°=190°﹣∠α, 解得:∠α=140°;
即当 a 为 125°或 110°或 140°时,△AOD 是等腰三角形.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 分别在函数
分别在函数![]() 与
与![]() 的图象上,
的图象上, ![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() 。
。

(1)若![]() 轴,求
轴,求![]() 的面积;
的面积;
(2)若![]() 是以
是以![]() 为底边的等腰三角形,且a
为底边的等腰三角形,且a![]() ,求
,求![]() 的值;
的值;
(3)作边长为2的正方形![]() ,使
,使![]() 轴,点
轴,点![]() 在点
在点![]() 的左上方,那么,对大于或等于的任意实数
的左上方,那么,对大于或等于的任意实数![]() ,
, ![]() 边与函数
边与函数![]() 的图象都有交点,请说明理由。
的图象都有交点,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1,x2是方程的两个实数根,且x12+x22=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
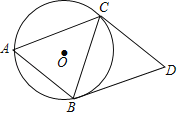
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售A、B两种文具,其中A文具的定价为20元/件,B产品的定价10元/件.
(1)若该文具按定价售出A、B两种文具共400件,若销售总额不低于5000元,则至少销售A产品多少件?
(2)该文具店2018年2月按定价销售A文具280件,B文具120件,2018年3月,市场情况发生变化,A文具销售价与上个月持平,但这个月的销售量比上个月减少了m%;B文具的销售价比上个月减少了m%,但销售量增加了![]() m%;3月份的销售总金额与2月份保持不变.求m的值.
m%;3月份的销售总金额与2月份保持不变.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
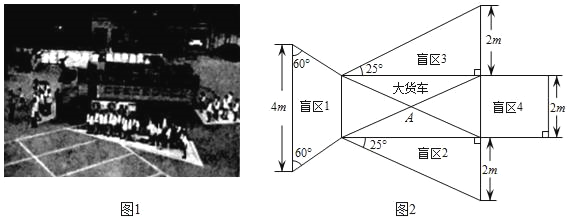
请你帮助小刚的学习小组解决下面的问题:
(1)盲区1的面积约是多少m2;盲区2的面积约是多少m2;
(![]() ≈1.4,
≈1.4,![]() ≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
(2)如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com