
����Ŀ��ij�ľߵ�����A��B�����ľߣ�����A�ľߵĶ���Ϊ20Ԫ/����B��Ʒ�Ķ���10Ԫ/����
��1�������ľ߰������۳�A��B�����ľ߹�400�����������ܶ����5000Ԫ������������A��Ʒ���ټ���
��2�����ľߵ�2018��2�°���������A�ľ�280����B�ľ�120����2018��3�£��г���������仯��A�ľ����ۼ����ϸ��³�ƽ��������µ����������ϸ��¼�����m%��B�ľߵ����ۼ۱��ϸ��¼�����m%����������������![]() m%��3�·ݵ������ܽ����2�·ݱ��ֲ��䣮��m��ֵ��
m%��3�·ݵ������ܽ����2�·ݱ��ֲ��䣮��m��ֵ��
���𰸡���1��100������2��m=15.
��������
��1��������A��Ʒx����������B��Ʒ��400-x�����������ܼ�=���ۡ�������������ܶ����500Ԫ�����ɵó�����x��һԪһ�β���ʽ����֮���ɵó�x��ȡֵ��Χ��ȡ���ڵ���Сֵ���ɵó����ۣ�
��2�������ܼ�=���ۡ��������3�·ݵ������ܽ����2�·ݱ��ֲ��䣬���ɵó�����m��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
�⣺��1��������A��Ʒx����������B��Ʒ��400��x������
������ã�20x+10��400��x����5000��
��ã�x��100��
����������A��Ʒ100����
��2����������ã�20��280��1��m%��+10��1��m%����120��1+![]() m%��=280��20+120��10��
m%��=280��20+120��10��
�����ã�8m2��120m=0��
��ã�m1=15��m2=0���������⣬��ȥ����
��m��ֵΪ15��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
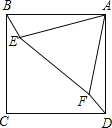
����Ŀ����ͼ��������ABCD����������AEF�Ķ���A�غϣ�����AEF�ƶ���A��ת������ת�����У���BE=DFʱ,��BAE�Ĵ�С������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
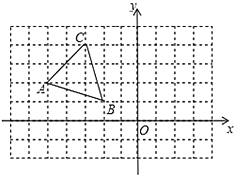
����Ŀ���ڱ߳�Ϊ1��С��������ɵ������������У�������ͼ��ʾ��ƽ���������ϵ����֪���������![]() �������ε��������㶼�ڸ���ϣ�
�������ε��������㶼�ڸ���ϣ�
��1������![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ����д����
�������![]() ��
��![]() ��
��![]() �����꣮
�����꣮
��2����ֱ��![]() ����һ��
����һ��![]() ��ʹ
��ʹ![]() ��С����ͼ���������������
��С����ͼ���������������![]() �㣨������ͼ�ۼ�������д����
�㣨������ͼ�ۼ�������д����![]() �����꣨��ʾ��ֱ��
�����꣨��ʾ��ֱ��![]() �ǹ���
�ǹ���![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ���ֱ�ߣ�
���ֱ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��һ�㣮
��һ�㣮
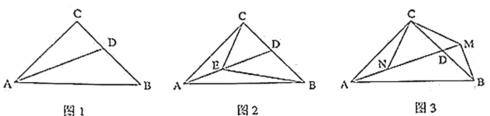
��1����ͼ![]() ��
��![]() ƽ��
ƽ��![]() ����֤��
����֤��![]() ��
��
��2����ͼ![]() ����
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ����֤��
����֤��![]() ��
��
��3����ͼ![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
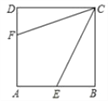
����Ŀ����ͼ��������ABCD�ı߳�Ϊ6����E��F�ֱ���AB��AD������CE=3![]() ���ҡ�ECF=45�㣬��CF��Ϊ�� ��
���ҡ�ECF=45�㣬��CF��Ϊ�� ��
A. 2![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��lAC��y=��![]() ��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��1�����B�����꼰ֱ��BC�Ľ���ʽ��
��2������OBC����BC�߷��ۣ��õ���O��BC������O����ֱ��O��E��ֱx���ڵ�E��F��y����һ�㣬P��ֱ��O��E������һ�㣬P��Q�������x��Գƣ���|PA��PC|���ʱ�������QF+![]() FC����Сֵ��
FC����Сֵ��
��3����M��ֱ��O��E��һ�㣬��QM=3![]() ���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ�������ͳ��ͼ�����ṩ����Ϣ����������⣺
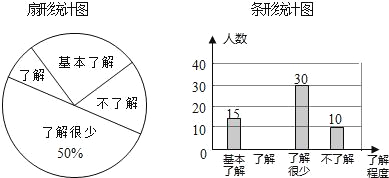
��1�������ʾ������ѧ�������� ���ˣ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
��2���벹ȫ����ͳ��ͼ��
��3��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��EΪCD���е㣬����AE��BE���ӳ�AE��BC���ӳ����ڵ�F��

��1����֤����DAE�ա�CFE��
��2����AB��BC+AD����֤��BE��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ������ͬһֱ���ϣ�����
������ͬһֱ���ϣ�����![]() ��
��

��1����![]() ����
����![]() ���ܳ���
���ܳ���
��2����ͼ![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��
����֤��![]() ��
��
��̽��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com