
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
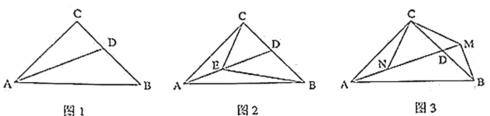
(1)如图![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() ;
;
(2)如图![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,求证:
,求证:![]() .
.
(3)如图![]() ,
,![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
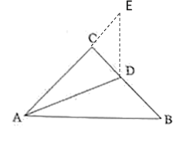
(1)延长AC至E,使CE=CD,利用AAS证出△BAD≌△EAD,从而得出AB=AE,即可证出结论;
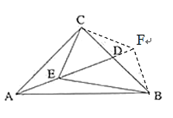
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF,先利用SAS证出△ACE≌△BCF,从而证出AE=BF,∠CEA=∠CFB,再证出∠EFB=90°,利用30°所对的直角边是斜边的一半即可证出结论;
(3)过点C作CE⊥AM于M,先利用AAS证出△CNA≌△CMB,即可证出CN=CM,根据等腰三角形的性质可得NE=EM,然后利用AAS证出△CED≌△BMD,从而得出ED=DM,然后根据线段的关系即可得出结论.
解:(1)延长AC至E,使CE=CD
∵![]() ,
,![]()
∴∠ECD=180°-∠ACB=90°,∠B=∠CAB=![]() (180°-∠ACB)=45°
(180°-∠ACB)=45°
∴△CDE为等腰三角形
∴∠E=45°
∴∠B=∠E
∵![]() 平分
平分![]()
∴∠BAD=∠EAD
在△BAD和△EAD中
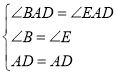
∴△BAD≌△EAD
∴AB=AE
∵AE=AC+CE=AC+CD
∴AB= AC+CD
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF
∵∠CED=45°
∴△CEF为等腰直角三角形
∴CE=CF,∠CFE=∠CEF=45°
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB,
∴∠ACE+∠ECB=90°,∠BCF+∠ECB=90°
∴∠ACE=∠BCF
在△ACE和△BCF中
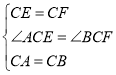
∴△ACE≌△BCF
∴AE=BF,∠CEA=∠CFB
∵∠CEA=180°-∠CEF=135°
∴∠CFB=135°
∴∠EFB=∠CFB-∠CFE=90°
在Rt△EFB中,∠BEF=30°
∴BE=2BF
∴BE=2AE
(3)过点C作CE⊥AM于M,
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB
∵CN⊥CM,BM⊥AM
∴∠NCM=90°,∠BMA=90°
∴∠ACN+∠NCB=90°,∠BCM+∠NCB=90°,
∴∠ACN=∠BCM
∴∠CNA=∠NCM+∠CMN=90°+∠CMN=∠CMB
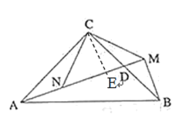
在△CNA和△CMB中
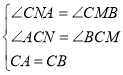
∴△CNA≌△CMB
∴CN=CM
∴△CNM为等腰直角三角形
∴NE=EM
在△CED和△BMD中
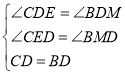
∴△CED≌△BMD
∴ED=DM
∴EM=2DM
∴NE=2DM
∴DN=NE+ED=3DM


科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
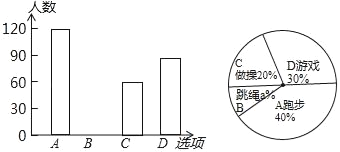
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
请结合统计图,回答下列问题:
(1)这次调查中,一共调查了多少名学生?
(2)求出扇形统计图中“B:跳绳”所对扇形的圆心角的度数,并补全条形图;
(3)若该校有2000名学生,请估计选择“A:跑步”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
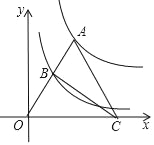
【题目】如图,点A为函数y=![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y=![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△OBC的面积为____.
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△OBC的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,若先由甲、乙两队合作![]() 天,剩下的工程再由乙队单独做
天,剩下的工程再由乙队单独做![]() 天可以完成,共需施工费
天可以完成,共需施工费![]() 万元;若由甲、乙合作完成此项工程共需
万元;若由甲、乙合作完成此项工程共需![]() 天,共需施工费
天,共需施工费![]() 万元.
万元.
(1)求乙队单独完成这项工程需多少天?
(2)甲、乙两队每天的施工费各为多少万元?
(3)若工程预算的总费用不超过![]() 万元,则乙队最少施工多少天?
万元,则乙队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
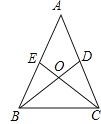
A.2种B.3种C.4种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售A、B两种文具,其中A文具的定价为20元/件,B产品的定价10元/件.
(1)若该文具按定价售出A、B两种文具共400件,若销售总额不低于5000元,则至少销售A产品多少件?
(2)该文具店2018年2月按定价销售A文具280件,B文具120件,2018年3月,市场情况发生变化,A文具销售价与上个月持平,但这个月的销售量比上个月减少了m%;B文具的销售价比上个月减少了m%,但销售量增加了![]() m%;3月份的销售总金额与2月份保持不变.求m的值.
m%;3月份的销售总金额与2月份保持不变.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(a)所示点D是等边![]() 边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边
边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边![]() ,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明.
,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明.
(2)如图(b)所示当动点D运动至等边![]() 边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?(直接写出结论)
边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?(直接写出结论)
(3)①如图(c)所示,当动点D在等边![]() 边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边
边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边![]() 和等边
和等边![]() ,连接AF、
,连接AF、![]() ,探究AF、
,探究AF、![]() 与AB有何数量关系?并证明.
与AB有何数量关系?并证明.
②如图(d)所示,当动点D在等边![]() 边BA的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.
边BA的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=![]() ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com