
【题目】两个工程队共同参与一项筑路工程,若先由甲、乙两队合作![]() 天,剩下的工程再由乙队单独做
天,剩下的工程再由乙队单独做![]() 天可以完成,共需施工费
天可以完成,共需施工费![]() 万元;若由甲、乙合作完成此项工程共需
万元;若由甲、乙合作完成此项工程共需![]() 天,共需施工费
天,共需施工费![]() 万元.
万元.
(1)求乙队单独完成这项工程需多少天?
(2)甲、乙两队每天的施工费各为多少万元?
(3)若工程预算的总费用不超过![]() 万元,则乙队最少施工多少天?
万元,则乙队最少施工多少天?
【答案】(1)乙队单独完成这项工程需90天;(2)甲队每天的施工费为15万元,乙队每天的施工费为8万元;(3)乙队最少施工30天
【解析】
(1)设乙队单独完成这项工程需x天,根据“甲、乙合作30天的工作量+乙队15天的工作量=1”列分式方程即可;
(2)设甲队每天的施工费为a万元,乙队每天的施工费为b万元,根据题意列二元一次方程组即可求出a、b的值;
(3)先求出甲的效率,设乙队施工y天,则甲队还需施工![]() 天完成任务,然后根据“总费用不超过
天完成任务,然后根据“总费用不超过![]() 万元”列出不等式即可得出结论.
万元”列出不等式即可得出结论.
解:(1)设乙队单独完成这项工程需x天
由题意可得:![]()
解得:x=90
经检验:x=90是原方程的解
答:乙队单独完成这项工程需90天.
(2)设甲队每天的施工费为a万元,乙队每天的施工费为b万元
由题意可知:
解得:![]()
答:甲队每天的施工费为15万元,乙队每天的施工费为8万元.
(3)甲的效率为![]()
设乙队施工y天,则甲队还需施工![]() 天完成任务
天完成任务
根据题意可得15×![]() +8y≤840
+8y≤840
解得:y≥30
答:乙队最少施工30天.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
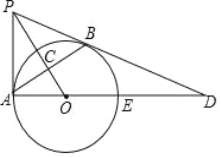
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
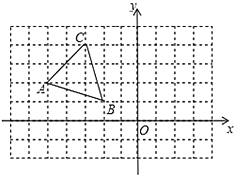
【题目】在边长为1的小正方形组成的正方形网格中,建立如图所示的平面真角坐标系,已知格点三角形![]() (三角形的三个顶点都在格点上)
(三角形的三个顶点都在格点上)
(1)画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;并写出点
;并写出点![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
(2)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 最小,在图中描出满足条件的
最小,在图中描出满足条件的![]() 点(保留作图痕迹),并写出点
点(保留作图痕迹),并写出点![]() 的坐标(提示:直线
的坐标(提示:直线![]() 是过点
是过点![]() 且垂直于
且垂直于![]() 轴的直线)
轴的直线)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
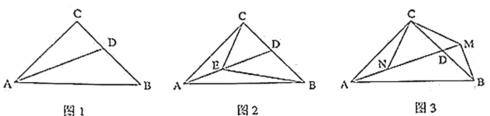
(1)如图![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() ;
;
(2)如图![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,求证:
,求证:![]() .
.
(3)如图![]() ,
,![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
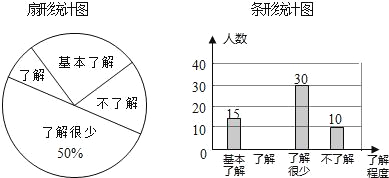
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com