
����Ŀ����ͼ1��ijѧУ��չ����ͨ��ȫ�ա�����ڻ�У�����������ͬѧ��չʾ�˴����ä���ķֲ�����������Ѵ�ң����ڼ�ʻ�ҵ�˾��������������ä���е�ͬѧ�ǣ�����һ��ҪԶ��������ä��������������ȫ��С�����ڵ�ѧϰС��Ϊ�˸��õķ��������ä�������⣬��ͼ1��ƽ��ͼ�ν��б�ʾ������ע�˲����������ݣ���ͼ2����ͼ2�д��������״Ϊ���Σ���ä��1Ϊ���Σ�ä��2��ä��3Ϊֱ�������Σ�ä��4Ϊ�����Σ�
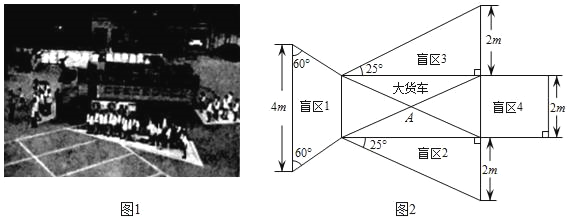
�������С�յ�ѧϰС������������⣺
��1��ä��1�����Լ�Ƕ���m2��ä��2�����Լ�Ƕ���m2��
��![]() ��1.4��
��1.4��![]() ��1.7��sin25���0.4��cos25���0.9��tan25���05���������������
��1.7��sin25���0.4��cos25���0.9��tan25���05���������������
��2������Դ����������A��ΪԲ�ģ���������ä���İ뾶��С��ԲΪ�������Σ����������ͼ2�л����������Σ������
���𰸡���1��ä��1�����Լ��5m2��ä��2�����Լ��4m2����2����AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ��������ͼ��ʾ������.
��������
��1����OP��CD��P�����ݵ������ε��������DP��![]() ��CD��OB����1����ֱ�ǡ�ODP���ó�OP��DPtan��D��
��CD��OB����1����ֱ�ǡ�ODP���ó�OP��DPtan��D��![]() �����������ε������ʽ�������ä��1���������ֱ�ǡ�BEN�����BE��
�����������ε������ʽ�������ä��1���������ֱ�ǡ�BEN�����BE��![]() ��4����ôS��BEN��
��4����ôS��BEN��![]() BEEN��4m2����Ϊä��2�������
BEEN��4m2����Ϊä��2�������
��2�����ù��ɶ������AC��AD��![]() ��
��![]() ��AH��AG��
��AH��AG��![]() ��
��![]() ��AM��AN��
��AM��AN��![]() ��
��![]() ���õ�AC�����ô��AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
���õ�AC�����ô��AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
��1����ͼ����OP��CD��P��
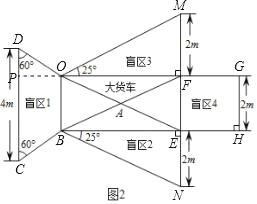
��OBCD�ǵ������Σ�OB��2��CD��4��
��DP��![]() ��CD��OB����1��
��CD��OB����1��
��ֱ�ǡ�ODP�У��ߡ�D��60�㣬
��OP��DPtan��D��1��![]() ��
��![]() ��
��
��S����OBCD��![]() ��OB+CD��OP��
��OB+CD��OP��![]() ��2+4��
��2+4��![]() ��3
��3![]() ��3��1.7��5��m2����
��3��1.7��5��m2����
��ä��1�����Լ��5m2��
��ֱ�ǡ�BEN�У��ߡ�EBN��25�㣬EN��2��
��BE��![]() ��4��
��4��
��S��BEN��![]() BEEN��
BEEN��![]() ��4��2��4��m2����
��4��2��4��m2����
��ä��2�����Լ��4m2��
�ʴ�Ϊ5��4��
��2����AC��AD��![]() ��
��
AH��AG��![]() ��
��
AM��AN��![]() ��
��
��AC��AD��AH��AG��AM��AN��
����AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
��ͼ��ʾ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� O �ǵȱ���ABC ��һ�㣬��AOB��110�㣬��BOC��a������BOC �Ƶ� C ��˳ʱ�뷽����ת 60������ADC������ADC�ա�BOC������ OD��
��1����֤����COD �ǵȱ������Σ�
��2��������120��ʱ�����ж� AD �� OC ��λ�ù�ϵ����˵�����ɣ�
��3��̽������ a Ϊ���ٶ�ʱ����AOD �ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����ABCΪ���������Σ�DΪCB�ӳ�����һ�㣬��AD�ҡ�DAC��45�㣬BD��1��CB��4����AC��Ϊ_____��
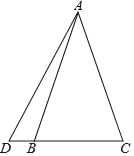
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʒ�̳�Ԥ��ijƷ���˶����ܹ�����������32000Ԫ������һ�������˶��������к�ܿ��������̳�����68000Ԫ�����ڶ��������˶��������������ǵ�һ������������2������ÿ���۶���10Ԫ��
��1�����̳����ι����������˶��������ף�
��2������������˶���ÿ���ۼ���ͬ����ȫ���������������![]() ����ôÿ���ۼ������Ƕ���Ԫ��
����ôÿ���ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C����������y=ax2��2amx+am2+2m��5�����Щ�![]() ��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��1����գ������ߵĶ�������Ϊ ���ú�m�Ĵ���ʽ��ʾ����
��2������ABC��������ú�a�Ĵ���ʽ��ʾ����
��3������ABC�����Ϊ2����2m��5��x��2m��2ʱ��y�����ֵΪ2����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ij�����ƻ��ڹ涨ʱ��������24000���������ÿ���ԭ�ƻ�������30����������ڹ涨ʱ���ڿ��Զ�����300�������
��1����ԭ�ƻ�ÿ����������������涨��������
��2��Ϊ����ǰ��������������ڰ���ԭ�й��˰�ԭ�ƻ�����������ͬʱ������5�������������ˮ�߹�ͬ���������������֪ÿ�������������ˮ��ÿ����������ĸ�����20������ԭ�ƻ�ÿ�������������������20%�����˲��㣬ǡ����ǰ�������24000�����������������ԭ�ƻ����ŵĹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶������ȤС�������ҿ�ͧȥɽ������죬���Ǵ�ͬһ��ͷ��������һ�ҿ�ͧ�ر�ƫ��70��������50ǧ�ף��ڶ��ҿ�ͧ����ƫ��20��������50ǧ�ף������ʱ��һ�ҿ�ͧ�������ڶ��ҿ�ͧ���һ�ҿ�ͧ��£����ô�ڶ��ҿ�ͧ���еķ���;���ֱ��ǣ�������
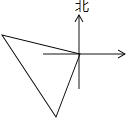
A. ��ƫ��![]() ��
��![]() ǧ�� B. ��ƫ��
ǧ�� B. ��ƫ��![]() ��
��![]() ǧ��
ǧ��
C. ��ƫ��![]() ��100ǧ�� D. ��ƫ��
��100ǧ�� D. ��ƫ��![]() ��100ǧ��
��100ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͬѧ��������·��AC����·��BD�������ߵ���Pʱ������������Ӱ�ӵĶ����պýӴ���·��AC�ĵײ���������ǰ�ٲ���20m����Q��ʱ��������ǰ��Ӱ�ӵĶ����պýӴ���·��BD�ĵײ�����֪����ͬѧ��������1.5m������·�Ƶĸ߶ȶ���9m������·��֮��ľ����ǣ��� ����

A. 24m B. 25m C. 28m D. 30m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ���ⳤΪ
���ⳤΪ![]() ��С��������ϳɵļ����壮
��С��������ϳɵļ����壮
![]() �ü����������ͼ��ͼ��ʾ���������淽��ֽ�зֱ���������ͼ����ͼ��
�ü����������ͼ��ͼ��ʾ���������淽��ֽ�зֱ���������ͼ����ͼ��
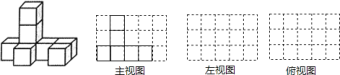
![]() ���������ı����Ϊ________
���������ı����Ϊ________![]() ��
��
![]() ����������������������һЩ��ͬ��С�����壬���������������ĸ���ͼ������ͼ���䣬��ô��������������л�������С����������ü��������п��ܵ�����ͼ��
����������������������һЩ��ͬ��С�����壬���������������ĸ���ͼ������ͼ���䣬��ô��������������л�������С����������ü��������п��ܵ�����ͼ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com