
【题目】已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为_____.
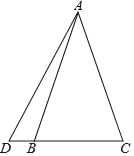
【答案】2![]()
【解析】
作辅助线,构建正方形AHGF,则AF=GH=GF,设GC=x,则FG=AF=HG=x+2,DG=x-1,在Rt△DGC中,利用勾股定理列方程可求得x的值,最后利用勾股定理计算AC的长即可.
解:过A作AE⊥DC于E,将△AEC沿AC翻折得△AFC,将△ADE沿AD翻折得△ADH,延长FC、HD交于G,
则∠EAC=∠CAF,∠EAD=∠HAD,∠H=∠F=90°,
∴∠EAC+∠EAD=∠CAF+∠HAD,
∵∠DAC=45°,即∠EAC+∠EAD=45°,
∴∠HAF=90°,
∴四边形AHGF是矩形,
∵AH=AE,AE=AF,
∴AH=AF,
∴四边形AHGF是正方形,
∴AF=GH=GF,
∵AB=AC,AE⊥BC,
∴BE=EC=2,
由折叠得:FC=EC=2,HD=DE=3,
设GC=x,则FG=AF=HG=x+2,
∴DG=x-1,
在Rt△DGC中,DC2=DG2+GC2,
52=(x-1)2+x2,
解得:x1=4,x2=-3(舍),
∴AF=x+2=4+2=6,
Rt△ACF中,AC=2![]()
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
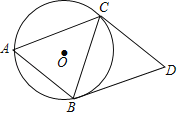
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售A、B两种文具,其中A文具的定价为20元/件,B产品的定价10元/件.
(1)若该文具按定价售出A、B两种文具共400件,若销售总额不低于5000元,则至少销售A产品多少件?
(2)该文具店2018年2月按定价销售A文具280件,B文具120件,2018年3月,市场情况发生变化,A文具销售价与上个月持平,但这个月的销售量比上个月减少了m%;B文具的销售价比上个月减少了m%,但销售量增加了![]() m%;3月份的销售总金额与2月份保持不变.求m的值.
m%;3月份的销售总金额与2月份保持不变.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销甲、乙两种商品,现有如下信息:
信息1:甲商品的零售单价比乙商品的零售单价少1元;
信息2:按零售单价购买甲商品3件和乙商品2件,共付了12元.
请根据以上信息,解答下列问题:
(1)分别求甲、乙两种商品的零售单价;
(2)该商店平均每天卖出甲、乙两种商品各500件,经调查发现,两种商品零售单价每降0.1元,甲种商品每天可多销售30件,乙种商品每天可多销售20件,商店决定把两种商品的零售单价均下降m(0<m<1)元.在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品的销售额之和为2500元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为非负实数,关于x的方程x2﹣(k+1)x+k=0和kx2﹣(k+2)x+k=0.
(1)试证:前一个方程必有两个非负实数根;
(2)当k取何值时,上述两个方程有一个相同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
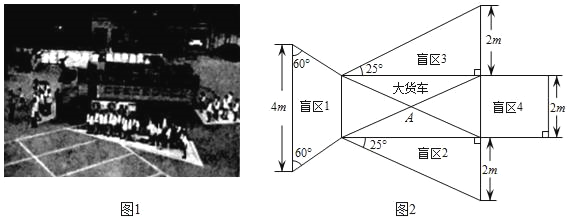
请你帮助小刚的学习小组解决下面的问题:
(1)盲区1的面积约是多少m2;盲区2的面积约是多少m2;
(![]() ≈1.4,
≈1.4,![]() ≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
(2)如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调厂的装配车间计划组装9000台空调.
(1)从组装空调开始,每天组装的台数m(单位:台/天)与生产时间t(单位:天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前10天上市,那么原装配车间每天至少要组装多少台空调?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com