
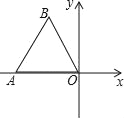
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
【答案】(﹣![]() ,﹣
,﹣![]() )
)
【解析】
作BC⊥x轴于C,如图,根据等边三角形的性质得OA=OB=1,AC=OC=![]() ,
,
∠BOA=60°,则易得A点坐标和O点坐标,再利用勾股定理计算出BC=![]() ,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B关于x轴对称,于是可得点A′的坐标.
,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B关于x轴对称,于是可得点A′的坐标.
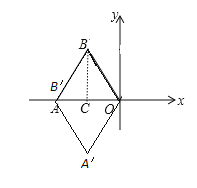
作BC⊥x轴于C,如图,∵△ABO是边长为1的等边三角形,
∴OA=OB=1,AC=OC=![]() ,∠BOA=60°,
,∠BOA=60°,
∴A点坐标为(-1, 0),O点坐标为(0, 0),
在Rt△BOC中,BC=![]() ,
,
∴B点坐标为(![]() ,
,![]() );
);
∵将△ABO按逆时针方向旋转60°,得到△OA′B′,
∴∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,
∴点B′与点A重合,点A′与点B关于x轴对称,即点A′的坐标为(![]() ,
,![]() ).
).
故答案为:![]() ,
,![]() ).
).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.
(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.
(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )
A.
B.
C.
D.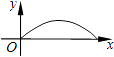
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).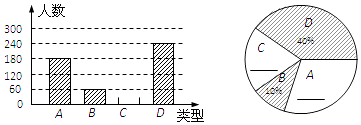
请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距120km.甲、乙两辆汽车同时从A地出发去B地,已知甲车的速度是乙车速度的1.2倍,结果甲车比乙车提前20分钟到达,求甲车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
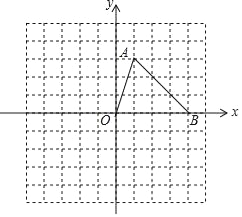
【题目】如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).
(1)画出将△ABO向左平移4个单位长度,再向上平移2个单位长度后得到的△A1B1O1;
(2)在(1)中,若△ABC上有一点M(3,1),则其在△A1B1O1中的对应点M1的坐标为 ;
(3)若将(1)中△A1B1O1看成是△ABO经过一次平移得到的,则这一平移的距离是 ;
(4)画出△ABO关于点O成中心对称的图形△A2B2O.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列函数: ①y=2﹣3x;②y=﹣ ![]() (x>0);③y=x﹣2;④y=2x2﹣1(x>1),
(x>0);③y=x﹣2;④y=2x2﹣1(x>1),
其中y随x的增大而增大的函数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com