
【题目】已知等腰△OPQ的顶点P的坐标为(4,3),O为坐标原点,腰长OP=5,点Q位于y轴正半轴上,则点Q的坐标为_____.
【答案】(0,6)或(0,5)
【解析】
分PO=PQ及OP=OQ两种情况考虑:①当PO=PQ时,过点P作PM⊥y轴于点M,由点P的坐标可得出点M的坐标,再利用等腰三角形的性质可求出点Q的坐标;②当OP=OQ时,利用两点间的距离公式(勾股定理)可得出OP的长度,再利用等腰三角形的性质可得出点Q的坐标.综上即可得出结论.
分两种情况考虑,如图所示.
①当PO=PQ时,过点P作PM⊥y轴于点M.
∵点P的坐标为(4,3),
∴点M的坐标为(0,3).
又∵PO=PQ,
∴OQ=2OM=6,
∴点Q的坐标为(0,6);
②当OP=OQ时,∵点P的坐标为(4,3),
∴OP=![]() =5,
=5,
∴点Q的坐标为(0,5),
故答案为:(0,6)或(0,5).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣ ![]() (x﹣2)2﹣3,下列说法错误的是( )
(x﹣2)2﹣3,下列说法错误的是( )
A.图象的开口向下
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(2,﹣3)
D.图象与y轴的交点坐标为(0,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体![]() ,如图所示.
,如图所示.

(1)请画出这个几何体![]() 的三视图.
的三视图.
(2)若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
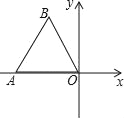
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
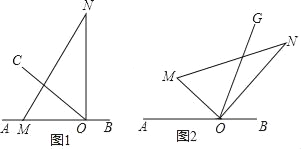
【题目】如图1,点O在直线AB上,∠AOC=30°,将一直角三角板的直角边OM与OA重合,ON在∠COB内部.现将三角板绕O沿顺时针方向以每秒2°的速度旋转,当ON与OB重合时停止转动.设运动时间为t(s).
(1)若直角边ON将∠COB分成∠CON:∠BON=3:2,求t的值;
(2)如图2,OG为三角板MON内部的射线,在旋转的过程中,OG始终平分∠MOB,请问∠AOM与∠NOG是否存在一定的数量关系?若存在,求出改数量关系;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
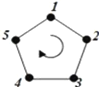
【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com