
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
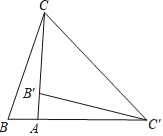
A. 33° B. 45° C. 57° D. 78°
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】现给出以下几个命题:
![]() 长度相等的两条弧是等弧;
长度相等的两条弧是等弧;![]() 相等的弧所对的弦相等;
相等的弧所对的弦相等;![]() 垂直于弦的直线平分这条弦并且平分弦所对的两条弧;
垂直于弦的直线平分这条弦并且平分弦所对的两条弧;![]() 钝角三角形的外接圆圆心在三角形外面;
钝角三角形的外接圆圆心在三角形外面;![]() 矩形的四个顶点必在同一个圆上.其中真命题的个数有( )
矩形的四个顶点必在同一个圆上.其中真命题的个数有( )
A. 1 个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1,x2是方程的两个实数根,且x12+x22=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
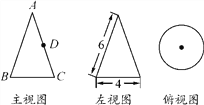
【题目】如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)已知a=1,C为抛物线与y轴的交点,若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
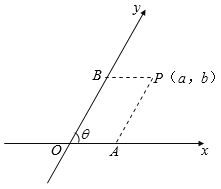
【题目】如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
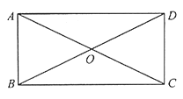
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是两根木棒及其影子的情形.

(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
材料2.已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2-x-1=0的两个不相等的实数根,
根据材料1得m+n=1,mn=-1,
∴![]() .
.
解决问题:
(1)一元二次方程x2-4x-3=0的两根为x1,x2,则x1+x2= ,x1x2= .
(2)已知实数m,n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com