【题目】如图，AB是⊙O的直径，弦AD，BC相交于点P，AD=BC．
（1）求证：△ACB≌△BDA；
（2）若∠ABC=35
，则∠CAP= ．
【答案】（1）答案见解析；（2）20．
【解析】
试题分析: （1）先根据圆周角定理得出∠ACB=∠BDA=90°，再由HL定理即可得出结论；
（2）先根据直角三角形的性质得出∠BAC的度数，再由圆周角定理得出∠BAD的度数，进而可得出结论．
试题解析:
(1)证明：∵AB是O的直径，
∴∠ACB=∠BDA=90°.
在Rt△ACB与Rt△BDA中，
∵
，
∴Rt△ACB≌Rt△BDA(HL)；
(2)∵AB是O的直径，
∴∠ACB=90°.
∵∠ABC=35°，
∴∠BAC=90°35°=55°.
∵Rt△ACB≌Rt△BDA，
∴弧AC=弧BD，
∴∠BAD=35°，
∴∠CAP=∠BAC∠BAD=55°35°=20°.
故答案为：20.
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案科目：初中数学 来源： 题型：
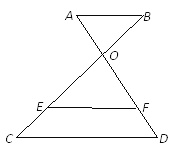
【题目】如图，已知AB∥EF∥CD，AD与BC相交于点O.
（1）如果CE=3，EB=9，DF=2，求AD的长；
（2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛一枚均匀硬币正面朝上的概率为
，下列说法错误的是
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币，平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目：初中数学 来源： 题型：
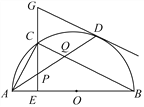
【题目】如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是
的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE，CB于点P，Q，连接AC，关于下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心，其中结论正确的是________(只需填写序号)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，他们共做了60次试验，试验的结果如下：
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我区某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个足球和篮球为关注儿童戍长的健康，实施“关注肥胖守儿童计划”，某校结全校各班肥胖儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：
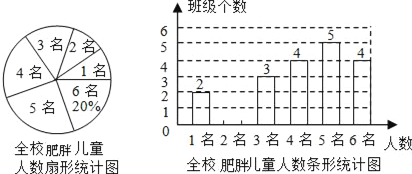
（1）全校班级个数 个 ，并将该条形统计图补充完整；
（2）为了了解肥胖儿重的饮食情况，某校决定从只有2名留守儿童的这些班级中，任选两名进行调查，请用列表法或画树形图的方法，求出所选两名肥胖儿童来自同一个班级的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上的点D处，折痕交OA于点C，则弧AD的长为（ ）
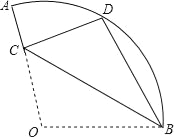
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
，
，对角线
、
交于点
，点
在
延长线上，联结
，
，
分别交线段、边
、对角线于点
、
、
（点不与点
、重合）．
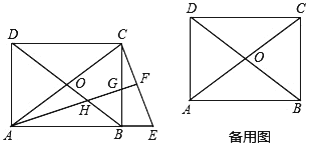
（1）当点是线段的中点，求
的长；
（2）设
，
，求
关于x的函数解析式，并写出它的定义域；
（3）当
是等腰三角形时，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，二次函数
的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．
（1）求m的值；
（2）求点B的坐标；
（3）该二次函数图像上有一点D（x，y）（其中
，
），使
，求点D的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com