
【题目】某校团委组织了有奖征文活动,并设立了一、二、三等奖,根据设奖情况买了50 件奖品,其二等奖奖品的件数比一等奖奖品的件数的2 倍少10, 各种奖品的单价如下表所示:

如果计划一等奖奖品买x件,买5 件奖品的总数是y元.
(1)先填表,再用含x的代数式表示y并化简;
(2)若一等奖奖品买10件,则共花费多少?
【答案】(1)二等奖是:2x﹣10(件),三等奖是: 60﹣3x(件);用含有 x 的代数式表示 y 是17x+100;(2)当 x=10 时,y=370元.
【解析】
根据表内信息,一等奖x件,由题意,二等奖是(2x-10)件,三等奖是[50-x-(2x-10)]件,即(60-3x)件,根据二、三等奖件数填表即可.
(1)根据“单价×数量=总价”分别求出买一、二、三等奖的总价,买一、二、三等奖的总价之和就是买50件奖品的总钱数.
(2)根据“单价×数量=总价”,即可求出一等奖奖品买10件,共花费多少元.
(1)二等奖是:2x-10(件),
三等奖是:50-x-(2x-10)
=50-x-2x+10
=60-3x(件),
填表如下:
一等奖奖品 | 二等奖奖品 | 三等奖奖品 | |
单价/元 | 12 | 10 | 5 |
数量/件 | x | 2x-10 | 60-3x |
用含有x的代数式表示y是:
y=12x+(2x-10)×10+(60-3x)×5
=12x+20x-200+300-15x
=17x+100;
(2)当x=10时,y=17×10+200=370(元).
答:若一等奖奖品买10件,共花费370元.


科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( ) 
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题: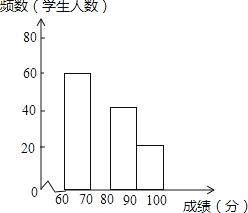
(1)在表中的频数分布表中,m= , n= .
成绩 | 频数 | 频率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).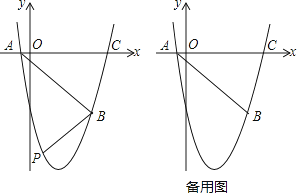
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数-20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记。
![]()
比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC......
(1)点A与点C之间的距离记作AC,求AC的长;
若数轴上有一点D满足CD=AD,求D点表示的数;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为![]() 秒.
秒.
①若点A向右运动,点C向左运动,AB=BC,求![]() 的值.
的值.
②若点A向左运动,点C向右运动,![]() 的值不随时间
的值不随时间![]() 的变化而改变,求
的变化而改变,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠1=∠2.
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内.
15;0.81;-![]() ,﹣3;﹣3.1;17;0;3.14
,﹣3;﹣3.1;17;0;3.14
正数集合{_______________________};
负数集合{_______};
整数集合{_________};
分数集合{_______________________};
有理数集合{_____________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣![]() )2019 的值.
)2019 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
有一些相同的房间需要粉刷,一天 3名一级技工去粉刷 8个房间,结果其中有 50![]() 墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40
墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40![]() 墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10
墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10![]() 墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?
墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com