
����Ŀ����ͼ���������ϵ�A��ʾ��-20����C��ʾ��30�����ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ���ǡ�
![]()
���磬��A���B֮��ľ������AB����B���C֮��ľ������BC......
��1����A���C֮��ľ������AC����AC�ij���
����������һ��D����CD=AD����D���ʾ������
��2������B����1��Ӧ�ĵ㿪ʼ�����˶����ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��A��C���������˶�����A��C���ٶȷֱ�Ϊÿ��2����λ���ȣ�ÿ��3����λ���ȣ��˶�ʱ��Ϊ![]() ��.
��.
������A�����˶�����C�����˶���AB=BC����![]() ��ֵ.
��ֵ.
������A�����˶�����C�����˶���![]() ��ֵ����ʱ��
��ֵ����ʱ��![]() �ı仯���ı䣬��
�ı仯���ı䣬��![]() ��ֵ.
��ֵ.
���𰸡���1��AC=50��D��ʾ5����2����t=![]() ��10 �� m=3
��10 �� m=3
��������
��1��![]() ��ֵ���뼴�ɣ�
��ֵ���뼴�ɣ�![]() �������.
�������.
��2���ٸ���·��=�ٶ�xʱ��,�Լ������ľ��빫ʽ����
�ڸ���������ʽ��6-2m=0ʱ,����ʽ��ֵ����ʱ��t�ı仯���ı䣬�ɵ�m=3��
��1��![]() ��
��![]() ��D=5.
��D=5.
��2��������ͼ��ʾ:

��t=0ʱ��AB=21��BC=29.
������������������:
a��A, C������ǰʱ��

��A, B֮��ÿ����С1����λ��������B �� Cÿ����С4����λ����.
��t=0ʱ�� BC -AB=8��
���AB=BC����ôAB-BC=0 ����ʱt=![]() ����
����

b.��A�� C������ʱ, AB= BC��
��A��C֮��ÿ����С5����λ���ȣ�
��t=0ʱ�� AC=50��
t=![]() = 10�룬
= 10�룬
c.��A, C��������BC����AC ,����������.
��������, t=![]() ��10.
��10.
�ڵ�ʱ��Ϊtʱ��
��A��ʾ����Ϊ-20+2t��
��B��ʾ����1+t��
��C��ʾ����Ϊ30+3t��![]()
![]() ��
��
��6-2m=0ʱ����ʽ��ֵ����ʱ��ı仯���ı䣬��ʱm=3.


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
�������߶εij��ȿ������߶ζ˵��ʾ�������м�������õ�������ͼ���߶�AB��1��0������1�����߶� BC��2��2��0���߶� AC��3��2������1������
�������ϵ�M��N���������ֱ�Ϊ��9��1�����߶�MN�� ��
�������ϵ�E��F���������ֱ�Ϊ��6�ͩ�3�����߶�EF�� ��
�������ϵ�������֮��ľ���Ϊ5������һ�����ʾ����Ϊ2������һ�����ʾ����Ϊm����m��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A.��������״����С���ʵ���ȫһ����5�������1��������������һ����һ���Ǻ���
B.����Ԥ�������콵ˮ����10%������ָ������10%��ʱ�������
C.ij�ط���һ�ָ�����Ʊ���н�����ǧ��֮һ����ô�������ֲ�Ʊ1000�ţ�һ�����н�
D.������һö����Ӳ�ң���5�ζ������泯�ϣ����������Ȼ�������泯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ί��֯���н����Ļ����������һ���������Ƚ��������轱�������50 ����Ʒ������Ƚ���Ʒ�ļ�����һ�Ƚ���Ʒ�ļ�����2 ����10�� ���ֽ�Ʒ�ĵ������±���ʾ��

����ƻ�һ�Ƚ���Ʒ��x������5 ����Ʒ��������yԪ��
��1������������ú�x�Ĵ���ʽ��ʾy������
��2����һ�Ƚ���Ʒ��10�������Ѷ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�У�AB=AD��AB��AD������AC������A��AE��AC����ʹAE=AC������BE����A��AH��CD��H��BE��F��
��1����ͼ1����E��CD���ӳ�����ʱ����֤���١�ABC�ա�ADE����BF=EF��
��2����ͼ2����E����CD���ӳ�����ʱ��BF=EF����������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У�AD=8��AEƽ�֡�BAD��BC�ڵ�E��DFƽ�֡�ADC��BC�ڵ�F����EF=2����AB�ij�Ϊ��������
A.3
B.5
C.2��3
D.3��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��I�ǡ�ABC�����ģ�AI���ӳ��ߺ͡�ABC�����Բ�ཻ�ڵ�D������BI��BD��DC������˵���д����һ���ǣ������� 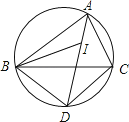
A.�߶�DB�Ƶ�D˳ʱ����תһ�������߶�DC�غ�
B.�߶�DB�Ƶ�D˳ʱ����תһ�������߶�DI�غ�
C.��CAD�Ƶ�A˳ʱ����תһ�������DAB�غ�
D.�߶�ID�Ƶ�I˳ʱ����תһ�������߶�IB�غ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com