
【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
【答案】D
【解析】解:①如图1,在ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB﹣EF=8,
∴AB=5;
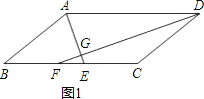
②在ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB+EF=8,
∴AB=3;
综上所述:AB的长为3或5.
故选D.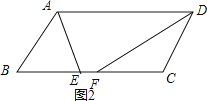
根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.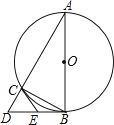
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数-20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记。
![]()
比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC......
(1)点A与点C之间的距离记作AC,求AC的长;
若数轴上有一点D满足CD=AD,求D点表示的数;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为![]() 秒.
秒.
①若点A向右运动,点C向左运动,AB=BC,求![]() 的值.
的值.
②若点A向左运动,点C向右运动,![]() 的值不随时间
的值不随时间![]() 的变化而改变,求
的变化而改变,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内.
15;0.81;-![]() ,﹣3;﹣3.1;17;0;3.14
,﹣3;﹣3.1;17;0;3.14
正数集合{_______________________};
负数集合{_______};
整数集合{_________};
分数集合{_______________________};
有理数集合{_____________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
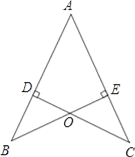
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣![]() )2019 的值.
)2019 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(直接写出结果)
(1)(﹣6)+(﹣14)=
(2)﹣8﹣(﹣8)=
(3)12+(﹣15)=
(4)+(+16)﹣(+4)=
(5)0﹣(﹣7)=
(6)﹣4×(﹣5)=
(7)0×(﹣15)=
(8)﹣15÷(﹣![]() )=
)=
(9)(﹣3)3=
(10)﹣52=
查看答案和解析>>
科目:初中数学 来源: 题型:
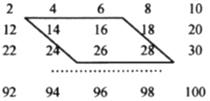
【题目】如图所示的数阵是由50个偶数排成的.
(1)图中框内的4个数有什么关系?
(2)在数阵图中任意作一类似于(1)中的框,设其中的一个数为![]() ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?
(3)如果四个数的和是172,能否求出这4个数?
(4)如果四个数的和是322,能否求出这4个数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com