练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．下列计算正确的是（　　）
    A．a+a2=a3B．a2•a3=a6C．（a2）3=a5D．a4÷a2=a2

    分析 根据同底数幂的乘法，可判断A、B，根据幂的乘方，可判断C，根据同底数幂的除法，可判断D．

    解答 解：A、不是同底数幂的乘法指数不能相加，故A错误；
    B、同底数幂的乘法底数不变指数相加，故B错误；
    C、幂的乘方底数不变指数相乘，故C错误；
    D、同底数幂的除法底数不变指数相减，故D正确；
    故选：D．

    点评 本题考查了同底数幂的除法，熟记法则并根据法则计算是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．已知分式$\frac{x-2}{x+3}$的值为0，则x的值为（　　）
    A．2B．-2C．3D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

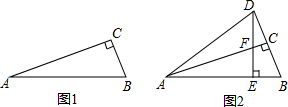    7．如图1，在△ABC中，∠C=90°，AB=1，∠A=α，则cosα=$\frac{AC}{AB}=AC$，现将△ABC沿AC折叠，得到△ADC，如图2，易知B、C、D三点共线，∠DAB=2α（其中0°＜α＜45°）．
    过点D作DE⊥AB于点E．
    ∵∠DCA=∠DEA=90°，∠DFC=∠AFE，
    ∴∠BDE=∠BAC=α，
    ∵BD=2BC=2sinα，
    ∴BE=BD•sinα=2•sinα•sinα=2sin2α，
    ∴AE=AB-BE=1-2sin2α，
    ∴cos2α=cos∠DAE=$\frac{AE}{AD}=\frac{1-2si{n}^{2}α}{1}=1-2si{n}^{2}α$．
    阅读以上内容，回答下列问题：
    （1）如图1，若BC=$\frac{1}{3}$，则cosα=$\frac{2\sqrt{2}}{3}$，cos2α=$\frac{7}{9}$；
    （2）求出sin2α的表达式（用含sinα或cosα的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．若a+b=2$\sqrt{2}$，ab=2，则a2+b2=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知一次函数y=（3a-2）x+（1-b）
    （1）当a，b为何值时，y随x的增大而增大？
    （2）当a，b为何值时，函数图象与y轴交于负半轴？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

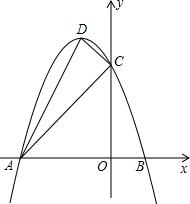    1．如图，二次函数y=ax2+bx+c（a＜0）图象的顶点为D，与x轴的两个交点分别为A、B（A在B左侧），与y轴交于点C（0，3），且OA=3OB，∠ACD=90°
    （1）求该二次函数的关系式；
    （2）若⊙M经过A、C、D三点，试求点B到⊙M的切线长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

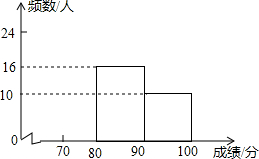    8．为了让读书成为习惯，某中学开展了读书征文比赛．经过评选，共有50篇征文获奖．现将评奖情况统计如下：
    等级成绩（用S表示）频数频率
    一等奖90≤S≤10010a
    二等奖80≤S＜9016b
    三等奖70≤S＜80c0.48
    合计501
    请根据以上提供的信息，解答下列问题：
    （1）求出统计表中a，b，c的值；
    （2）补全频数分布直方图；
    （3）若初一年级的两男、两女四名同学获得一等奖，现从四人中随机抽取两人让他们谈谈参赛体会，请用画树状图或列表的方法求出恰好抽到两名男生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

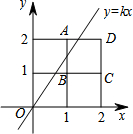    5．将2×2的正方形网格如图放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上．若直线y=kx（k≠0）与正方形ABCD有公共点，则k的取值范围是（　　）
    A．k≤2B．$k≥\frac{1}{2}$C．$\frac{1}{2}≤k≤2$D．$\frac{1}{2}＜k＜2$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）$\sqrt{18}$+$\sqrt{12}$-$\sqrt{8}$-$\sqrt{27}$
    （2）$\sqrt{45}$+3$\sqrt{\frac{1}{2}}$-$\frac{1}{2}$$\sqrt{20}$-$\sqrt{0.125}$
    （3）（3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$）÷$\sqrt{32}$．

    查看答案和解析>>

    同步练习册答案