
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π). 分析 贴纸部分的面积等于扇形ABC减去小扇形ADE的面积,已知圆心角的度数为120°,扇形的半径为25cm和25-15=10cm,可根据扇形的面积公式求出贴纸的面积.
解答 解:设AB=R,AD=r,
则S贴纸=$\frac{1}{3}$πR2-$\frac{1}{3}$πr2
=$\frac{1}{3}$π(R2-r2)
=$\frac{1}{3}$π(R+r)(R-r)
=$\frac{1}{3}$×(25+10)×(25-10)π
=175π(cm2).
答:贴纸的面积为175πcm2.
故答案为:175π.
点评 本题主要考查扇形面积的计算的应用,解答本题的关键是熟练掌握扇形面积计算公式,此题难度一般.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
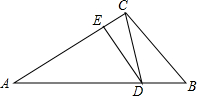 如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.
如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
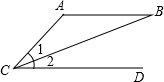 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.
如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (-3)2=6 | C. | (-a3)2=a6 | D. | a2+a3=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
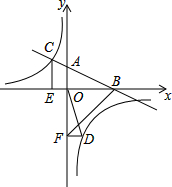 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com