
【题目】如图,有人在岸上点C的地方,用绳子拉船靠岸开始时,绳长CB=5米,拉动绳子将船身向岸边行驶了2米到点D后,绳长CD=![]() 米,求岸上点C离水面的高度CA.
米,求岸上点C离水面的高度CA.

【答案】3米.
【解析】试题分析:
设AD= ![]() 米,则由题意可知:AB=BD+AD=
米,则由题意可知:AB=BD+AD=![]() 米,∠CAB=90°,由此根据勾股定理可得:在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,由此可得:CB2-AB2=CD2-AD2,即:
米,∠CAB=90°,由此根据勾股定理可得:在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,由此可得:CB2-AB2=CD2-AD2,即: ![]() ,解方程求得
,解方程求得![]() 的值,将所求
的值,将所求![]() 的值代入:AC2=CD2-AD2即可求得AC的值.
的值代入:AC2=CD2-AD2即可求得AC的值.
试题解析:
由题意可知:∠CAB=90°,
∴在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,
∴CB2-AB2=CD2-AD2.
设AD= ![]() 米,则由题意可知:AB=BD+AD=
米,则由题意可知:AB=BD+AD=![]() 米,
米,
∴![]() ,解得:
,解得: ![]() ,即AD=2米.
,即AD=2米.
∴AB=2+2=4(米),
∴AC2=CB2-AB2=25-16=9,
∴AC=3(米).
答:点C离水面高度AC为3米.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】某城市按以下规定收取每月的煤气费:用气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费,已知某用户6月份煤气费平均每立方米0.88元,那么,6月份这位用户应交煤气费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程![]() 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.

查看答案和解析>>
科目:初中数学 来源: 题型:
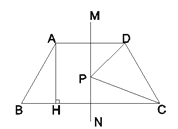
【题目】如图,题型ABCD中,AD∥BC,AD=CD=AD=2,∠B=60°,AH⊥BC于点H,且AH=![]() ,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com