
【题目】下列是小朋友用火柴棒拼出的一组图形:

仔细观察,找出规律,解答下列各题:
(1)第四个图中共有 根火柴棒,第六个图中共有 根火柴棒;
(2)按照这样的规律,第n个图形中共有 根火柴棒(用含n的代数式表示);
(3)按照这样的规律,第20个图形中共有多少根火柴棒?
【答案】(1)13,19;(2)(3n+1)根;(3)有61根火柴棒.
【解析】试题分析:
分析已知的四个图形中的火柴数量可得:
第1个图形中火柴根数为:4+0×1=4(根);
第2个图形中火柴根数为:4+3×1=7(根);
第3个图形中火柴根数为:4+3×2=10(根);
第4个图形中火柴根数为:4+3×3=13(根);
……;
由此可得:第n个图形中火柴根数为:4+3×(n-1)=(3n+1)(根).
根据上面结论即可计算得出(1)至(3)问的答案.
试题解析:
(1)根据图形分析可得第四个图案中火柴棒有:3×4+1=13(根);
第六个图案中火柴棒有:3×6+1=19(根).
故答案为13,19.
(2)观察、分析上述图形可得:
当n=1时,火柴棒的根数是4+3×0=4;
当n=2时,火柴棒的根数是4+3×1=7;
当n=3时,火柴棒的根数是4+3×2=10;
当n=4时,火柴棒的个数是4+3×3=13;
…;
所以第n个图形中共有火柴棒的根数为:4+3×(n-1)=(3n+1)(根).
(3)由(2)中结论可知:
当n=20时,3n+1=3×20+1=61.
∴ 第20个图形中共有61根火柴棒.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(2,0),抛物线的对称轴x=-1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形BOCF的面积最大,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名.在期末考试中,他们又是班上的前四名.如果他们当中只有一位的排名与期中考试中的排名相同,那么排名情况有( )种可能.
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
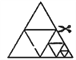
【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
A. 332 B. 333 C. 334 D. 335
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( ) 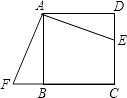
A.4
B.8
C.16
D.无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
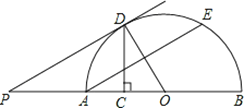
【题目】如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是![]() 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com