

分析 (1)根据圆周角定理可知∠BAE+∠EBA=90°,由∠BAE=∠BDE,∠BDE=∠CBE,所以∠EBA+∠EBC=90°.
(2)易证OD∥DE,从而可知$\frac{PD}{DE}=\frac{PO}{OB}$,易证△EDF∽△BDE,DE2=DF•DB,从而可求出DB的长度,由勾股定理可知AB的长度.
解答 解:(1)∵AB是直径,
∴∠BAE+∠EBA=90°,
∵∠BAE=∠BDE,∠BDE=∠CBE,
∴∠EBA+∠EBC=90°,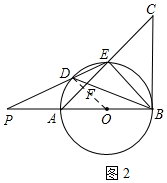
∴BC是⊙O的切线,
(2)连接OD,
∵BD平分∠ABE,
∴∠OBD=∠EBD,
∵∠ODB=∠OBD,
∴∠ODB=∠DBE,
∴OD∥BE,
∵PA=AO
∴$\frac{PD}{DE}=\frac{PO}{OB}=2$,
∵∠DEF=∠DBA,
∴∠DEF=∠EBD,
∵∠EDF=∠EDB,
∴△EDF∽△BDE,
∴$\frac{DE}{DF}=\frac{DB}{DE}$,
∴DE2=DF•DB,
∴DB=$\frac{9}{2}$,
∴由勾股定理可知:AB2=AD2+BD2,
∴AB=$\frac{3\sqrt{13}}{2}$,
∴AO=$\frac{3\sqrt{13}}{4}$
点评 本题考查元的综合问题,涉及相似三角形的性质与判定,切线的判定,圆周角定理、勾股定理等知识,综合程度较高,需要灵活运用所学知识.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
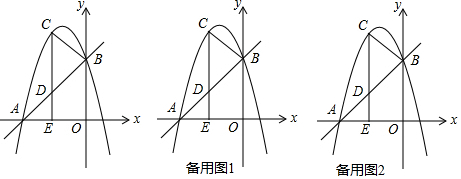
 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A左B右),交y轴于点C,直线y=x分别交抛物线于D、E,连接BD,且OD=4$\sqrt{2}$,OB=4
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A左B右),交y轴于点C,直线y=x分别交抛物线于D、E,连接BD,且OD=4$\sqrt{2}$,OB=4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com