
 ��ͼ��������y=-$\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣨A��B�ң�����y���ڵ�C��ֱ��y=x�ֱ���������D��E������BD����OD=4$\sqrt{2}$��OB=4
��ͼ��������y=-$\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣨A��B�ң�����y���ڵ�C��ֱ��y=x�ֱ���������D��E������BD����OD=4$\sqrt{2}$��OB=4���� ��1������ȷ��D��B�������꣬���ô���ϵ�������ɽ�����⣻
��2�����÷����������E���꣬���������μ��ɽ�����⣻
��3���ӳ�PG��BD��F����PM��y�ύBD��M��GN��y�ύBD��N����AB��K���ɡ�OBG�ǵ��������Σ���֪G��2��2����ֱ��BD�Ľ���ʽΪy=$\frac{1}{2}$x-2������֤��PM=2GN����֪N��2��-1����GN=3���Ƴ�PM=6=��-$\frac{1}{2}$m2+$\frac{1}{2}$m+6��-��$\frac{1}{2}$m-2��=6���ⷽ�̼��ɽ�����⣮
��� �⣺��1�� ��D��ֱ��y=x�ϣ�OD=4$\sqrt{2}$��
��D��ֱ��y=x�ϣ�OD=4$\sqrt{2}$��
��D��-4��-4����
��OB=4��
��B��4��0����
��D��-4��-4����B��4��0������y=-$\frac{1}{2}$x2+bx+c�õ�$\left\{\begin{array}{l}{-8-4b+c=-4}\\{-8+4b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=\frac{1}{2}}\\{c=6}\end{array}\right.$��
��y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+6��
��2��������P��m��-$\frac{1}{2}$m2+$\frac{1}{2}$m+6����N��m��m����
��$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+6}\\{y=x}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-4}\\{y=-4}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$��
��E��3��3����
�ٵ�-4��m��3ʱ��d=-$\frac{1}{2}$m2+$\frac{1}{2}$m+6-m=-$\frac{1}{2}$m2-$\frac{1}{2}$m+6��
�ڵ�3��m��4ʱ��d=m-��-$\frac{1}{2}$m2+$\frac{1}{2}$m+6��=$\frac{1}{2}$m2+$\frac{1}{2}$m-6��
��3���ӳ�PG��BD��F����PM��y�ύBD��M��GN��y�ύBD��N����AB��K��
��D��-4��-4����B��4��0����
�ߡ�OBG�ǵ��������Σ���֪G��2��2����
ֱ��BD�Ľ���ʽΪy=$\frac{1}{2}$x-2��
��PG=GH��
���GPH=��GHP��
�ߡ�GPH+��PFH=90�㣬��GHF+��GHP=90�㣬
���GHF=��GFH��
��HG=GP=FG��
��GN��PM��
��MN=FM��
��PM=2GN��
��֪N��2��-1����GN=3��
��PM=6=��-$\frac{1}{2}$m2+$\frac{1}{2}$m+6��-��$\frac{1}{2}$m-2��=6��
���m=2��-2��
��P��2��5����-2��3����
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�ֱ�������ε����ʡ�ƽ���߷��߶γɱ���������֪ʶ������ؼ���ѧ�����ӳ��ø����ߣ�ѧ�����ò���������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
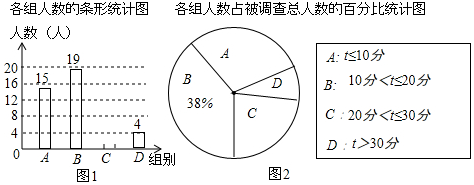
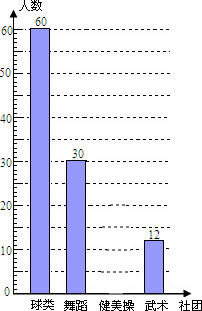 Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺| ������� | ���� | ռ���������� |
| ���� | 60 | m |
| �赸 | 30 | 0.25 |
| ������ | n | 0.15 |
| ���� | 12 | 0.1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=2x+2��ֱ��y=-2x+6���ڵ�P�����Ƿֱ���x�ύ��A��B��
��ͼ��ֱ��y=2x+2��ֱ��y=-2x+6���ڵ�P�����Ƿֱ���x�ύ��A��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 80�� | C�� | 90�� | D�� | 100�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com