
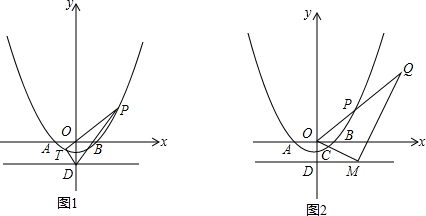
分析 (1)将抛物线的解析式设为两点式,再将C点坐标代入即可求出;
(2)作PM垂直定直线于M,可计算出PM=PO=PQ,即∠OMQ=90°,由于垂线段的唯一性,垂足也就是唯一的,结论显然;
(3)作TE垂直定直线于E,作PF垂直定直线于F,只需证∠EDE=∠PDF即可,即只需证$\frac{TE}{ED}=\frac{PF}{FD}$即可,因此设出直线PT的解析式,及P、T两点的坐标,将这四条线段用坐标表示.由于P、T是直线与抛物线的交点,故联立方程组,得出韦达定理结论,参与线段运算.通过运算,$\frac{TE}{ED}=\frac{PF}{FD}$肯定是成立的,从而结论自然成立.
解答 解:(1)
设抛物线的解析式为y=a(x+1)(x-1),
将C点坐标代入可解得:a=$\frac{1}{2}$,
∴$y=\frac{1}{2}{x}^{2}-\frac{1}{2}$,
(2)作PM与定直线垂直,M为垂足,如图1,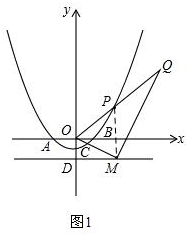
设P(t,$\frac{1}{2}{t}^{2}-\frac{1}{2}$),则PM=$\frac{1}{2}{t}^{2}+\frac{1}{2}$,
∵OP=$\sqrt{{t}^{2}+(\frac{1}{2}{t}^{2}-\frac{1}{2})^{2}}$=$\frac{1}{2}{t}^{2}+\frac{1}{2}$,
∴PM=PO=PQ,∴∠OMQ=90°
根据“过直线外一点有且仅有一条直线与已知直线垂直”可知,M是唯一的,
也就是说,以P为圆心,PO为半径的圆恰好与定直线y=-1相切于点M,切点M当然是唯一的,
故在直线y=-1上有且仅有一点M,使∠OMQ=90°.
(3)设直线PT的解析式为y=kx,作TE与定直线垂直,垂足为E,作PF与定直线垂直,垂足为F,如图2,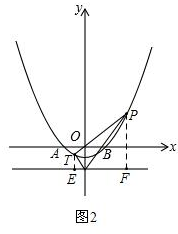
设P(x1,y1),T(x2,y2),
由$\left\{\begin{array}{l}{y=kx}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}}\end{array}\right.$消法y整理得:x2-2kx-1=0,
由韦达定理可知:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2k}\\{{x}_{1}•{x}_{2}=-1}\end{array}\right.$,
又$\frac{TE}{ED}=\frac{{y}_{2}+1}{-{x}_{2}}$,$\frac{PF}{DF}=\frac{{y}_{1}+1}{{x}_{1}}$,
$\frac{{y}_{1}+1}{{x}_{1}}+\frac{{y}_{2}+1}{{x}_{2}}$=$\frac{k{x}_{1}+1}{{x}_{1}}+\frac{k{x}_{2}+1}{{x}_{2}}$=$\frac{2k{x}_{1}•{x}_{2}+{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{-2k+2k}{-1}$=0,
∴$\frac{TE}{ED}=\frac{PF}{DF}$,
∴∠TDE=∠PDF,
∴∠ODT=∠ODP,
即:y轴平分∠PDT.
点评 本题考查了待定系数法求抛物线解析式、两点间的距离公式、直角形三角形斜边中线定理逆定理、韦达定理、相似三角形的判定与性质等知识点,技巧性很强,有一定难度.事实上,本题以一种巧妙的方式考查了抛物线的解析性质,(2)(3)问的解答过程也体现了解析特性,这里用到的解答技巧在高中解析几何的学习过程中会继续用到,务必引起重视.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=-(x-m)2+n.
已知函数y=-(x-m)2+n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
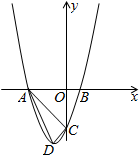 如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴相交于点C(0,-3)与x轴交于A、B两点(点A在点B的左边),连接AC、CD、AD.
如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴相交于点C(0,-3)与x轴交于A、B两点(点A在点B的左边),连接AC、CD、AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
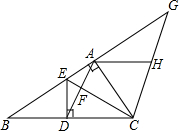 在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交干点E,EC与AD相交于点F,过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交干点E,EC与AD相交于点F,过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com