Question

6．在△ABC中，AB、BC的垂直平分线相交于三角形内一点O，下列结论中，错误的是（　　）

• A． 点O在AC的垂直平分线上
• B． △AOB、△BOC、△COA都是等腰三角形
• C． ∠OAB+∠OBC+∠OCA=90°
• D． 点O到AB、BC、CA的距离相等

Answer 1

分析 根据垂直平分线的性质得：O也是AC垂直平分线上的点，则O到三个顶点的距离相等，可以得△AOB、△BOC、△COA都是等腰三角形，且根据等边对等角得：∠OAB=∠ABO，∠OBC=∠OCB，∠OAC=∠OCA，再由三角形内角和定理得：∠OAB+∠OBC+∠OCA=90°；
三角形的角平分线的交点到三边的距离相等．

解答 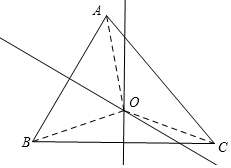解：A、连接AO、BO、CO，
∵AB、BC的垂直平分线相交于三角形内一点O，
∴AO=BO，BO=CO，
∴AO=CO，
∴点O在AC的垂直平分线上，
所以选项A正确；
B、∵AO=BO，BO=CO，AO=CO，
∴△AOB、△BOC、△COA都是等腰三角形，
所以选项B正确；
C、∵AO=BO，BO=CO，AO=CO，
∴∠OAB=∠ABO，∠OBC=∠OCB，∠OAC=∠OCA，
∵∠BAC+∠ABC+∠ACB=180°，
∴∠OAB+∠OBC+∠OCA=90°，
故选项C正确；
D、∵点O是三边垂直平分线的交点，
∴OA=OB=OC，
但点O到AB、BC、CA的距离不一定相等；
所以选项D错误；
本题选择错误的，
故选D．

点评 本题主要考查线段垂直平分线的性质，还考查了等腰三角形的性质和判定及角平分线的性质，熟练掌握线段垂直平分线的性质是关键，注意三角形三边垂直平分线的交点是外心，它到三个顶点的距离相等．