【题目】如图，∠1＋∠2=180°，∠A=∠C，DA平分∠BDF．
（1）求证：AE∥CF．
（2）BC平分∠DBE吗？为什么？
【答案】（1）见详解；（2）BC平分∠DBE，证明见详解．
【解析】
（1）根据同角的补角相等，证明∠2=∠DBE，问题得证；
（2）先证明AD∥BC，进而证明∠C=∠CBD，再根据AE∥CF，证明∠CBD=∠CBE，问题得证．
解：（1）证明：∵∠1＋∠2=180°，∠1＋∠DBE=180°，
∴∠2=∠DBE，
∴AE∥CF；
（2）BC平分∠DBE，
证明：∵AE∥CF，
∴∠C+∠CBA=180°，
∵∠A=∠C，
∴∠A+∠CBA=180°，
∴AD∥BC，
∴∠ADB=∠CBD，∠FDA=∠C，
∵DA平分∠BDF，
∴∠FDA=∠ADB，
∴∠C=∠CBD，
∵AE∥CF，
∴∠C=∠CBE，
∴∠CBD=∠CBE，
∴BC平分∠DBE．
科目：初中数学 来源： 题型：
【题目】完成推理过程
（1）如图，已知∠1=∠2，∠B=∠C，求证：AB∥CD．
证明∵∠1=∠2(已知)，
且∠1=∠CGD( )
∴∠2=∠CGD( )，
∴CE∥BF( )，
∴∠C=∠BFD( )
又∵∠B=∠C(已知)，
∴∠BFD=∠B( )，
∴AB∥CD( )
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．
（1）求证：直线BD与⊙O相切；
（2）若AD：AE＝4：5，BC＝6，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为8的等边三角形ABC中，点D沿射线AB方向由A向B运动，点F同时从C出发，以相同的速度每秒1个单位长度沿射线BC方向运动，过点D作DE⊥AC，连结DF交射线AC于点G．
（1）当DF⊥AB时，求AD的长；
（2）求证：EG＝
AC．
（3）点D从A出发，经过几秒，CG＝1.6？直接写出你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2
（1）如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．
（2）利用（1）中所得到的结论，解决下面的问题： 已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值．
（3）如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，铜亭广场装有智能路灯，路灯设备由灯柱AC与支架BD共同组成（点C处装有安全监控，点D处装有照明灯），灯柱AC为6米，支架BD为2米，支点B到A的距离为4米，AC与地面垂直，∠CBD=60°．某一时刻，太阳光与地面的夹角为45°，求此刻路灯设备在地面上的影长为多少？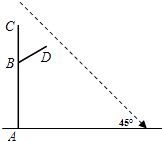
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=BC，CD⊥AB于点D，CD=BD，BE平分∠ABC，点H是BC边的中点，连接DH，交BE于点G．
（1）求证：△ADC≌△FDB；
（2）求证：CE=
BF；
（3）连结CG，判断△ECG的形状，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
