
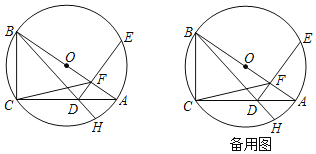
【题目】如图,![]() 是
是![]() 的内接三角形,AB为
的内接三角形,AB为![]() 直径,
直径,![]() ,
,![]() ,点D为线段AC上一动点,过点D作AB的垂线交
,点D为线段AC上一动点,过点D作AB的垂线交![]() 于点E,交AB于点F,连结BD,CF,并延长BD交
于点E,交AB于点F,连结BD,CF,并延长BD交![]() 于点H.
于点H.
![]() 求
求![]() 的半径;
的半径;
![]() 当DE经过圆心O时,求AD的长;
当DE经过圆心O时,求AD的长;
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
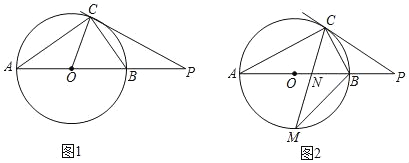
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
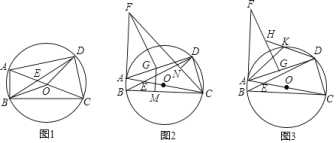
【题目】已知,四边形ABCD内接于![]() ,对角线AC和BD相交于点E,AC是
,对角线AC和BD相交于点E,AC是![]() 的直径.
的直径.
![]() 如图1,连接OB和OD,求证:
如图1,连接OB和OD,求证:![]() ;
;
![]() 如图2,延长BA到点F,使
如图2,延长BA到点F,使![]() ,在AD上取一点G,使
,在AD上取一点G,使![]() ,连接FG和FC,过点G作
,连接FG和FC,过点G作![]() ,垂足为M,过点D作
,垂足为M,过点D作![]() ,垂足为N,求
,垂足为N,求![]() 的值;
的值;
![]() 如图3,在
如图3,在![]() 的条件下,点H为FG的中点,连接DH交
的条件下,点H为FG的中点,连接DH交![]() 于点K,连接AK,若
于点K,连接AK,若![]() ,
,![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
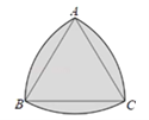
【题目】如图,分别以等边三角形 ABC 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形就是“勒洛三角形”(勒洛 三角形是定宽曲线所能构成的面积最小的图形),若 AB=2,则勒洛三角形的面积为( )
A. π+ ![]() B. π-
B. π-![]() C. 2π+2
C. 2π+2 ![]() D. 2π-2
D. 2π-2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为⊙O 的直径,PD 切⊙O 于点 C,交 AB 的延长线于点 D,且∠D=2∠A.
(1)求∠D 的度数;
(2)若⊙O 的半径为 m,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方米15000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米12150元的均价开盘销售
![]() 求平均每次下调的百分率.
求平均每次下调的百分率.
![]() 某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
![]() 打
打![]() 折销售;
折销售;![]() 不打折,一次性送装修费每平方米250元.
不打折,一次性送装修费每平方米250元.
试问哪种方案更优惠?比另外一种方案优惠多少元?![]() 不考虑其他因素
不考虑其他因素![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
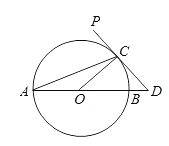
【题目】某校对A《唐诗》、B《宋词》、C《蒙山童韵》、D其它,这四类著作开展“最受欢迎的传统文化著作”调查,随机调查了若干名学生(每名学生必选且只能选这四类著作中的一种)并将得到的信息绘制了下面两幅不完整的统计图:
(1)求一共调查了多少名学生;
(2)请将条形统计图补充完整;
(3)该校语文老师想从这四类著作中随机选取两类作为学生寒假必读书籍,请用树状图或列表的方法求恰好选中《宋词》和《蒙山童韵》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
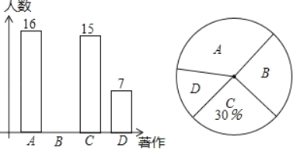
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com