
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
【答案】(1)y=2x﹣5,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)利用两点间的距离公式求出AB的长,利用点到直线的距离公式求出点C到直线AB的距离,即可确定出三角形ABC面积.
试题解析:(1)把A(2,﹣1)代入反比例解析式得:﹣1=![]() ,即m=﹣2,∴反比例解析式为
,即m=﹣2,∴反比例解析式为![]() ,把B(
,把B(![]() ,n)代入反比例解析式得:n=﹣4,即B(
,n)代入反比例解析式得:n=﹣4,即B(![]() ,﹣4),把A与B坐标代入y=kx+b中得:
,﹣4),把A与B坐标代入y=kx+b中得: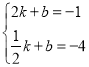 ,解得:k=2,b=﹣5,则一次函数解析式为y=2x﹣5;
,解得:k=2,b=﹣5,则一次函数解析式为y=2x﹣5;
(2)∵A(2,﹣1),B(![]() ,﹣4),直线AB解析式为y=2x﹣5,∴AB=
,﹣4),直线AB解析式为y=2x﹣5,∴AB=![]() =
=![]() ,原点(0,0)到直线y=2x﹣5的距离d=
,原点(0,0)到直线y=2x﹣5的距离d=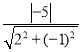 =
=![]() ,则S△ABC=
,则S△ABC=![]() ABd=
ABd=![]() .
.


科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小敏在研究绝对值的问题时,遇到了这样一道题:
(1)当式子|x﹣1|+|x+5|取最小值时,x应满足的条件是 , 此时的最小值是 . 小聪说:利用数轴求线段的长可以解决这个问题.如图,点A,B对应的数分别为﹣5,1,则线段AB的长为6,我发现也可通过|1﹣(﹣5)|或|﹣5﹣1|来求线段AB的长,即数轴上两点间的线段的长等于它们所对应的两数差的绝对值.![]()
小敏说:我明白了,若点C在数轴上对应的数为x,线段AC的长就可表示为|x﹣(﹣5)|,那么|x﹣1|表示的是线段的长.
小聪说:对,求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值,而点C在线段AB上时AC+BC=AB最小,最小值为6.
小敏说:点C在线段AB上,即x取﹣5,1之间的有理数(包括﹣5,1),因此相应x的取值范围可表示为﹣5≤x≤1时,最小值为6.
请你根据他们的方法解决下面的问题:
(2)小敏说的|x﹣1|表示的是线段的长;
(3)当式子|x﹣3|+|x+2|取最小值时,x应满足的条件是;
(4)当式子|x﹣2|+|x+3|+|x+4|取最小值时,x应满足的条件是;
(5)当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|(a<b<c<d)取最小值时,x应满足的条件是 , 此时的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
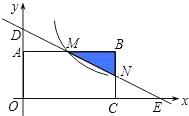
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数![]() (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数![]() (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com