
【题目】小聪和小敏在研究绝对值的问题时,遇到了这样一道题:
(1)当式子|x﹣1|+|x+5|取最小值时,x应满足的条件是 , 此时的最小值是 . 小聪说:利用数轴求线段的长可以解决这个问题.如图,点A,B对应的数分别为﹣5,1,则线段AB的长为6,我发现也可通过|1﹣(﹣5)|或|﹣5﹣1|来求线段AB的长,即数轴上两点间的线段的长等于它们所对应的两数差的绝对值.![]()
小敏说:我明白了,若点C在数轴上对应的数为x,线段AC的长就可表示为|x﹣(﹣5)|,那么|x﹣1|表示的是线段的长.
小聪说:对,求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值,而点C在线段AB上时AC+BC=AB最小,最小值为6.
小敏说:点C在线段AB上,即x取﹣5,1之间的有理数(包括﹣5,1),因此相应x的取值范围可表示为﹣5≤x≤1时,最小值为6.
请你根据他们的方法解决下面的问题:
(2)小敏说的|x﹣1|表示的是线段的长;
(3)当式子|x﹣3|+|x+2|取最小值时,x应满足的条件是;
(4)当式子|x﹣2|+|x+3|+|x+4|取最小值时,x应满足的条件是;
(5)当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|(a<b<c<d)取最小值时,x应满足的条件是 , 此时的最小值是 .
【答案】
(1)﹣5≤x≤1;6;BC
(2)BC
(3)﹣2≤x≤3
(4)x=﹣3
(5)b≤x≤c;c﹣b+d﹣a
【解析】解:(2)由题意可知:|x﹣1|=BC;(3)由题意可知:﹣2≤x≤3;(4)|x﹣2|+|x+3|+|x+4|表示数x分别与﹣4、﹣3、2的距离之和,由题意可知:当﹣3≤x≤2时,|x+3|+|x﹣2|可取得最小值,∴当x=﹣3时,|x﹣2|+|x+3|+|x+4|可取得最小值,(5)由题意可知:|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|表示数x分别与a、b、c、d的距离之和,∴b≤x≤c时,x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|的最小值为:c﹣b+d﹣a.所以答案是:(1)﹣5≤x≤1,6,BC(2)BC(3)﹣2≤x≤3(4)x=﹣3(5)b≤x≤c,c﹣b+d﹣a.根据绝对值的性质以及题意即可求出答案.
【考点精析】根据题目的已知条件,利用数轴和绝对值的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.


科目:初中数学 来源: 题型:
【题目】(10分)某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,增加下列条件后,ABCD不一定是菱形的是( ) 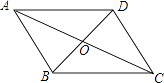
A.DC=BC
B.AC⊥BD
C.AB=BD
D.∠ADB=∠CDB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-x-1与x轴的一个交点的坐标为(m,0),则代数式m2-m+2019的值为( )
A. 2015B. 2016C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:正方形ABCD中,AB=8,点O为边AB上一动点,以点O为圆心,OB为半径的⊙O交边AD于点E(不与点A、D重合),EF⊥OE交边CD于点F.设BO=x,AE=y.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)在点O运动的过程中,△EFD的周长是否发生变化?如果发生变化,请用x的代数式表示△EFD的周长;如果不变化,请求出△EFD的周长;
(3)以点A为圆心,OA为半径作圆,在点O运动的过程中,讨论⊙O与⊙A的位置关系,并写出相应的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣1与反比例函数y= ![]() 的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 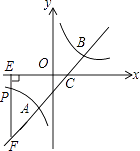
(1)反比例函数的解析式为 , 直线y=x﹣1在双曲线y= ![]() 上方时x的取值范围是;
上方时x的取值范围是;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),将线段AB先向上平移2个单位长度,再向右平移1个单位长度,得到线段CD,连接AC,BD,构成平行四边形ABDC.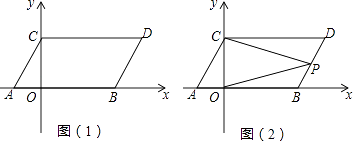
(1)请写出点C的坐标为 , 点D的坐标为 , S四边形ABDC;
(2)点Q在y轴上,且S△QAB=S四边形ABDC , 求出点Q的坐标;
(3)如图(2),点P是线段BD上任意一个点(不与B、D重合),连接PC、PO,试探索∠DCP、∠CPO、∠BOP之间的关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com