
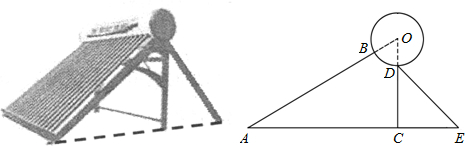
分析 首先弄清题意,了解每条线段的长度与线段之间的关系,在△CDE中利用三角函数sin60°求出求出CD的长,再设出水箱半径OD的长度为xcm,表示出CO,AO的长度,根据直角三角形的性质得到CO的长再代入数计算即可得到答案.
解答 解:∵在直角△CDE中,∠CED=60°,
∴tan60°=$\frac{CD}{CE}$=$\sqrt{3}$,
∴CE=$\frac{\sqrt{3}}{3}$CD,
设水箱半径OD的长度为xcm,则CO=(CD+x)cm,AO=(160+x)cm,
∵∠BAC=30°,
∴CO=$\frac{1}{2}$AO,AC=AO•cos30°=$\frac{\sqrt{3}}{2}$AO,
即CD+x=80+$\frac{1}{2}$x①
又$\frac{\sqrt{3}}{2}$AO+$\frac{\sqrt{3}}{3}$CD=200,即$\frac{\sqrt{3}}{2}$(160+x)+$\frac{\sqrt{3}}{3}$(80-$\frac{x}{2}$)=200
解得:x=160-76$\sqrt{3}$≈160-76×1.7=30.8,
答:水箱半径OD的长度约为30.8cm.
点评 此题主要考查了解直角三角形的应用,充分体现了数学与实际生活的密切联系,解题的关键是表示出线段的长后,理清线段之间的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
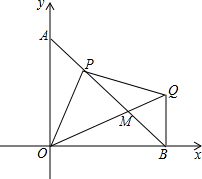 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com