
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
 从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题:
从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
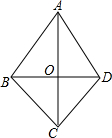 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
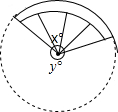 如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则x为( )
如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则x为( )| A. | 144° | B. | 135° | C. | 136° | D. | 108° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com