
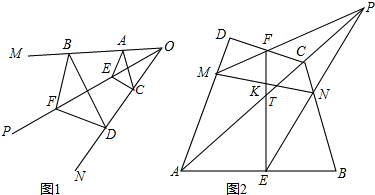
���� ��1������ƽ���߷��߶γɱ��������Ƴ����ۣ�
��2���������⣬��EF�ء�PMN����$\frac{NK}{KM}•\frac{MF}{FP}•\frac{PE}{EN}=1$ �٣���BC�ء�PAE����$\frac{EB}{BA}•\frac{AC}{CP}•\frac{PN}{NE}=1$ �ڣ�����$\frac{PN}{NE}=\frac{2CP}{AC}$���Ƴ�$\frac{PE}{EN}=\frac{2CP+AC}{AC}$ �ۣ���CD�ء�PMA����$\frac{FD}{DC}•\frac{CA}{AP}•\frac{PM}{MF}$=1��$\frac{PM}{MF}=\frac{2AP}{AC}$��֤��$\frac{PF}{MF}$=$\frac{2AP-AC}{AP}$ �ܣ�����ΪAP=AC+CP�����Եõ�2CP+AC=2AP-AC���ɢۡ��ܵ�$\frac{PE}{EN}=\frac{FP}{MF}$����$\frac{MF}{FP}•\frac{PE}{MF}=1$�������ɢٵã�NK=KM����K���߶�MN���е㣮
��� ֤������1����AE��BF��
��$\frac{OA}{OB}=\frac{OE}{OF}$��
��CE��DF��
��$\frac{OC}{OD}=\frac{OE}{OF}$��
��$\frac{OA}{OB}=\frac{OC}{OD}$��
��AC��BD��
�ߵ�E��OF���е㣬
��$\frac{OE}{OF}$=$\frac{1}{2}$��
��$\frac{OA}{OB}=\frac{OC}{OD}=\frac{AC}{BD}=\frac{1}{2}$��
��AC=$\frac{1}{2}$BD��
��2����EF�ء�PMN��
��$\frac{NK}{KM}•\frac{MF}{FP}•\frac{PE}{EN}=1$ �٣�
��BC�ء�PAE��
��$\frac{EB}{BA}•\frac{AC}{CP}•\frac{PN}{NE}=1$ �ڣ�
��$\frac{PN}{NE}=\frac{2CP}{AC}$��
��$\frac{PE}{EN}=\frac{2CP+AC}{AC}$ �ۣ�
��CD�ء�PMA��
��$\frac{FD}{DC}•\frac{CA}{AP}•\frac{PM}{MF}$=1
��$\frac{PM}{MF}=\frac{2AP}{AC}$��
��$\frac{PF}{MF}$=$\frac{2AP-AC}{AP}$ �ܣ�
��AP=AC+CP��
��2CP+AC=2AP-AC��
�ɢۡ��ܵ�$\frac{PE}{EN}=\frac{FP}{MF}$��
��$\frac{MF}{FP}•\frac{PE}{MF}=1$��
���ɢٵã�NK=KM��
��K���߶�MN���е㣮
���� ���⿼����ƽ���߷��߶γɱ����������߶ν����������õ��߶εı�Ϊ��ֵ���Լ����������ʣ�����Ĺؼ������߶ν����������õ��߶εıȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
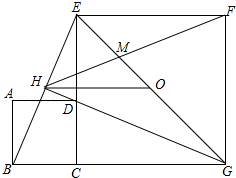 ��ͼ��������ABCD�ı�CD��������CEFG�ı�CE�غϣ���O��EG���е㣬��CGE��ƽ����GH����D����BE��H������OH��FH��EG��FH����M�����������ĸ����ۣ�
��ͼ��������ABCD�ı�CD��������CEFG�ı�CE�غϣ���O��EG���е㣬��CGE��ƽ����GH����D����BE��H������OH��FH��EG��FH����M�����������ĸ����ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
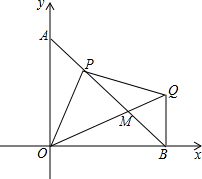 ��֪����ͼ��A��B��������Ϊ��0��4����B��4��0����PΪ�߶�AB�ϵ���һ�㣬��P��OP�Ĵ������B���x��Ĵ��߽��ڵ�Q��OQ��ֱ��AB���ڵ�M����̽������������⣺
��֪����ͼ��A��B��������Ϊ��0��4����B��4��0����PΪ�߶�AB�ϵ���һ�㣬��P��OP�Ĵ������B���x��Ĵ��߽��ڵ�Q��OQ��ֱ��AB���ڵ�M����̽������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
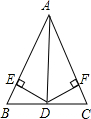 ��ͼ���ڡ�ABC�У�AD�ǡ�BAC��ƽ���ߣ�DE��AB��E��DF��AC��F��BD=DC����֤����B=��C��
��ͼ���ڡ�ABC�У�AD�ǡ�BAC��ƽ���ߣ�DE��AB��E��DF��AC��F��BD=DC����֤����B=��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| ��������Ĵ���m | 70 | 128 | 171 | 302 | 481 | 599 | 1806 |
| ���������Ƶ��$\frac{m}{n}$ | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
| A�� | ����1500�����������Ƶ�ʱ�����800�εĸ��ӽ�0.6 | |
| B�� | �Ӹú�������������һ��С����������ĸ���Ϊ0.6 | |
| C�� | ���������nΪ2000ʱ����������Ĵ���mһ������1200 | |
| D�� | ��������еİ�����28�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com