
【题目】已知:m2+2m-3=0.
求证:关于x的方程x2-2mx-2m=0有两个不相等的实数根.
【答案】原方程有两个不相等的实数根.
【解析】试题分析:
要证明该方程有两个不相等的实数根,需要证明该一元二次方程根的判别式的值大于零. 因此,应先求得该方程的根的判别式,再利用已知条件求其值,最后通过该判别式的值大于零证得该方程有两个不相等的实数根.
试题解析:
证明:根据关于x的方程x2-2mx-2m=0的形式可知该方程为关于x的一元二次方程.
对照此方程与一元二次方程的一般形式ax2+bx+c=0 (a,b,c为常数,a≠0) 可得一般形式中各常数的值:
a=1,b=-2m,c=-2m,
因此,该方程的根的判别式![]() ,
,
∵m2+2m-3=0,
∴m2+2m=3,
∴![]() ,
,
∵当一元二次方程根的判别式![]() 时,方程有两个不相等的实数根,
时,方程有两个不相等的实数根,
∴关于x的方程x2-2mx-2m=0有两个不相等的实数根.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛.在最近的10次选拔赛中,他们的成绩如下(单位:cm):
甲 | 585 | 596 | 610 | 598 | 612 | 597 | 604 | 600 | 613 | 601 |
乙 | 613 | 618 | 580 | 574 | 618 | 593 | 585 | 590 | 598 | 624 |
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的极差、方差分别是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
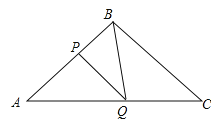
【题目】如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒。
(1)当x为何值时,PQ∥BC?
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)△APQ能否与△CQB相似?若能,求出时间x的值,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据宁波市统计局公布的第六次人口普查数据,本市常住人口760.57万人,其中760.57万人用科学记数法表示为( )
A.7.6057×105人
B.7.6057×106人
C.7.6057×107人
D.0.76057×107人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;
③3a+c=0; ④a﹣b<m(ma+b)(m≠﹣1的实数);
其中正确的命题是( )

A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华计划在十一长假期间每天做5道数学题,超过的题数记为正数,不足的题数记为负数.七天中的实际做题数记录如下:+3,+5,-4,-2,-1,+7,0.则小华七天共做了________道数学题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是( )
A.木条是直的
B.两点确定一线
C.过一点可以画出无数条直线
D.两点之间线段最短
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com