【题目】已知抛物线y=-x2+bx+c的部分图象如图所示，A(1，0),B(0，3).

（1）求抛物线的解析式；

（2）结合函数图象，写出当y<3时x的取值范围.

参考答案：

【答案】（1）；（2）x<-2或x>0．

【解析】试题分析：

(1) 从题目中所给出的图象可知，点A和点B这两个已知点均在该二次函数图象上. 因此，可以将点A与点B的坐标代入二次函数解析式并组成方程组，求得待定系数b与c的值，进而获得该二次函数的解析式.

(2) 在题目所给出的图象上作直线y=3，该直线交二次函数图象于两点. 观察图象易知，满足y<3的二次函数图象应该在直线y=3的下方. 根据这部分图象横坐标的特点可知满足条件的横坐标分布范围. 由于该取值范围由直线y=3与二次函数交点的横坐标确定，故可以联立两个解析式解得交点坐标，进而求得x的取值范围.

试题解析：

(1) 由题目中的图象可知：该二次函数的图象过点A(1, 0)，点B(0, 3)，

将点A与点B的坐标代入二次函数的解析式，得

，即，

解之，得

，

故该二次函数的解析式为.

(2) 将题目中给出的二次函数图象适当延长，作直线y=3交二次函数图象于点B，C. (如图)

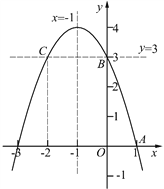
分析图象可知，满足y<3的二次函数图象应该是位于直线y=3下方的部分.

观察这部分图象上点的横坐标可知，对应y<3的x的取值应该小于点C的横坐标值或大于点B的横坐标值.

根据点B与点C均为该二次函数与直线y=3的交点可得下列方程组：

，

解这个方程组，得

,

，

∴x1=0，x2=-2.

即点B的坐标为(0, 3)，点C的坐标为(-2, 3).

综上所述，当y<3时x的取值范围为x<-2或x>0.

关闭