
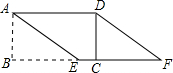
 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.分析 (1)根据平移的性质得到AE∥DF,AE=DF,则由此判定四边形AEFD是平行四边形;然后由“邻边相等的平行四边形是菱形”证得结论;
(2)根据勾股定理,可得答案.
解答 (1)证明:由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
又∵AE=AD=5,
∴四边形AEFD是菱形.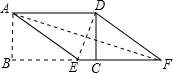
(2)依题意得:AB•AD=15,即5AB=15,
故AB=3.
在直角△ABE中,AB=3,AE=5,则由勾股定理得到:BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=4.
如图,连接AF,ED.
在直角△ABF中,由勾股定理得到:AF=$\sqrt{A{B}^{2}+(BE+EF)^{2}}$=$\sqrt{{3}^{2}+(4+5)^{2}}$=3$\sqrt{10}$.
在直角△DCE中,由勾股定理得到:DE=$\sqrt{D{C}^{2}+(BC-BE)^{2}}$$\sqrt{{3}^{2}+(5-4)^{2}}$=$\sqrt{10}$.
点评 本题考查了菱形的判定与性质、图形的剪拼以及平移的性质.通过解答该题,使学生学会能够灵活运用菱形、勾股定理知识解决有关问题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
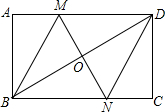 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
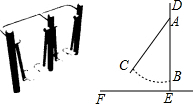 图中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°.求此时点C距离地面EF的高度.(结果精确到0.01m)【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
图中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°.求此时点C距离地面EF的高度.(结果精确到0.01m)【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】查看答案和解析>>
科目:初中数学 来源: 题型:填空题
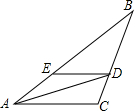 如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
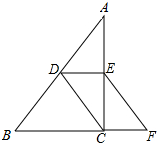 如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
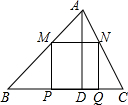 锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )| A. | 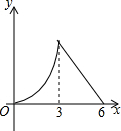 | B. | 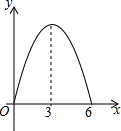 | C. | 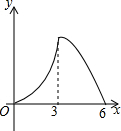 | D. | 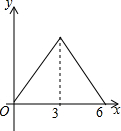 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
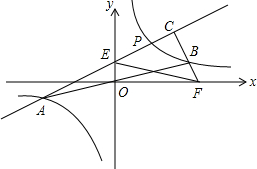 已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.
已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com