
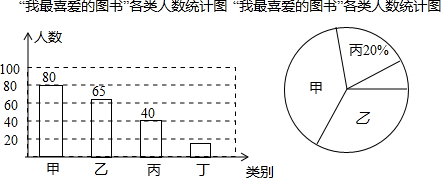
分析 (1)由丙的人数除以占的百分比求出调查的总学生数即可;
(2)由总学生数减去已知其他类的学生数求出丁类的学生数;
(3)利用甲类占的百分比乘总人数即可;
(4)用总人数乘最喜爱丁类图书的人数所占百分比即可.
解答 解:(1)40÷20%=200(名)
答:共调查的学生人为200名;
(2)根据题意得:丁类学生数为200-(80+65+40)=15(名);
(3)最喜爱甲类图书的人数占本次被调查人数的80÷200×100%=40%;
(4)1600×$\frac{15}{200}$=120(人)
答:该校最喜爱丁类图书的人数为120人.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图并能准确的画图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
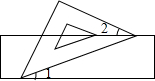 如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )
如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )| A. | 25° | B. | 20° | C. | 15° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
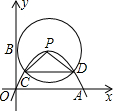 如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
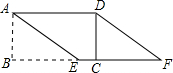 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com