
 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.分析 (1)根据待定系数法,将点A,点B代入抛物线解析式,解关于b,c的二元一次方程组,即可求得抛物线的解析式;
(2)根据待定系数法求出直线AC的解析式,设点P(m,m2+2m-8),用含m的式子表示出点D,将它们的纵坐标相减,用含m的式子表示出PD的长度,根据平行四边形的对边平行且相等,得PD=BC,求出m的值,即可求出点P的坐标;
(3)由题意,可知OA=OC,得到∠ACO=45°,根据平行线的性质及三角形的内角和,可得∠PDE=∠DPE=45°,进而得△DPE是等腰直角三角形,根据等腰三角形的三线合一和直线三角形斜边上的中线等于斜边的一半,可得:EF=$\frac{1}{2}$PD,用含m的式子表示出点E的横坐标,根据二次函数的最大值,即可解答.
解答 解:(1)抛物线y=x2+bx+c经过点A(-4,0),点B(0,8),
∴$\left\{\begin{array}{l}{16-4b+c=0}\\{c=-8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=-8}\end{array}\right.$,
∴这条抛物线所对应的函数表达式为y=x2+2x-8;
(2)设直线AC的解析式为:y=kx+b,点A(-4,0),点C(0,-4)在直线AC上,
∴$\left\{\begin{array}{l}{-4k+b=0}\\{b=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=-4}\end{array}\right.$,
∴直线AC所对应的函数表达式为:y=-x-4;
∵点P在抛物线y=x2+2x-8上,
∴设点P(m,m2+2m-8),
∵PD∥y轴,
∴点D(m,-m-4),
∴PD=-m-4-(m2+2m-8)=-m2-3m+4,
∵四边形PBCD是平行四边形,
∴PD=BC,即-m2-3m+4=4,解得:m1=0,m2=-3,
∵点P不与点B重合,
∴m=-3,
∴P(-3,-5);
(3)∵点A(-4,0),点C(0,-4),
∴OA=OC,
∵∠AOC=90°,
∴∠ACO=45°,
∵PD∥y轴,
∴∠PDE=∠ACO=45°,
∵PE⊥AC于点E,
∴∠PED=90°,
∴∠PDE=∠DPE=45°,
设点E的横坐标为n,如图,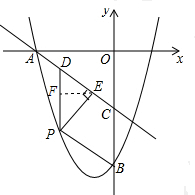
过点E作EF⊥PD于点F,
∵△DPE是等腰直角三角形,
∴EF=$\frac{1}{2}$PD,即n-m=$\frac{1}{2}$PD,
∴n=m+$\frac{1}{2}$PD=m+$\frac{1}{2}$(-m2-3m+4)=-$\frac{1}{2}$(m+$\frac{1}{2}$)2+$\frac{17}{8}$,
∵-4<m<0,
∴当m=-$\frac{1}{2}$时,n最大,且n的最大值为$\frac{17}{8}$.
点评 本题主要考查二次函数的综合应用,第(2)小题熟记平行四边形的对边平行且相等是解决此题的关键,第(3)小题,考查了等腰三角形和直线三角形的性质,能够将等腰三角形的三线合一和直角三角形斜边的中线等于斜边的一半联系起来是解决此题的关键.


科目:初中数学 来源: 题型:填空题
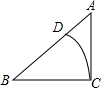 如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$.
如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
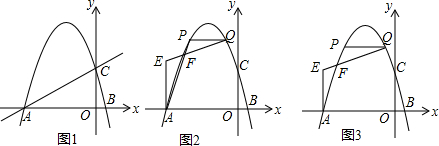
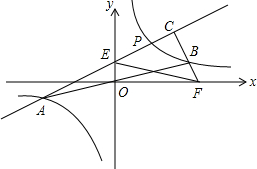 已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.
已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
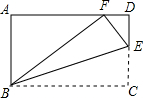 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
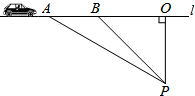 超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?
超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.
如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com