
已知:△ABC中,点E是AB边的中点,点F在AC边上,若以A,E, F为顶点的三角形与△ABC相似,则需要增加的一个条件是 .(写出一个即可)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 若两个扇形满足弧长的比等于
若两个扇形满足弧长的比等于 它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形
它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形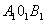 是相似扇形,且半径
是相似扇形,且半径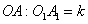 (
(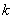 为不等于0的常数)。那么下面四个结论:
为不等于0的常数)。那么下面四个结论:
①∠AOB=∠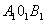 ;②△AOB∽△
;②△AOB∽△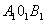 ;③
;③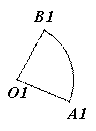
 ;
;
④扇形AOB与扇形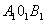 的面积之比为
的面积之比为 。成立的个数为:
。成立的个数为:
A、1个 B、2个 C、3个 D、4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,曲线 抛物线的一部分,且表达式为:
抛物线的一部分,且表达式为: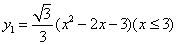 曲线
曲线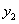 与曲线
与曲线 关于直线
关于直线 对称。
对称。
(1)求A、B、C三点的坐标和曲线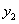 的表达式;
的表达式;
(2)过点D作 轴交曲线
轴交曲线 于点D,连接AD,在
于点D,连接AD,在 曲线
曲线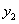 上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
(3)设直线CM与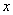 轴交于点N,试问在线段MN下方的曲线
轴交于点N,试问在线段MN下方的曲线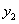 上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数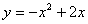 .有下列四个结论:①它的对称轴是直线
.有下列四个结论:①它的对称轴是直线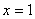 ;②设
;②设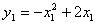 ,
,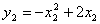 ,则当
,则当 时,有
时,有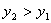 ;③它的图象与x轴的两个交点是(0,0)和(2,0);④当
;③它的图象与x轴的两个交点是(0,0)和(2,0);④当 时,
时, .其中正确的结论的个数为( )
.其中正确的结论的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
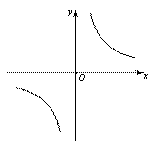
如图,过原点的直线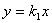 和
和 与反比例函数
与反比例函数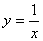 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时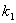 和
和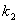 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(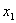 ,
,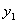 ),Q(
),Q( ,
,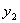 )(
)(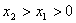 )是函数
)是函数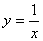 图象上的任意两点,
图象上的任意两点,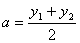 ,
,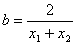 ,试判断
,试判断 ,
, 的大小关系,并说明理由.
的大小关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
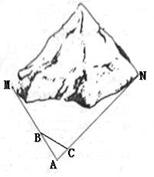
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞, 工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com