
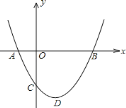
【题目】如图,二次函数![]() 图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程
图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程![]() 的两根是-1和3.在下面结论中:①abc>0;②a+b+c<0;③c+3a=0;④若点M(
的两根是-1和3.在下面结论中:①abc>0;②a+b+c<0;③c+3a=0;④若点M(![]() ,m)在此抛物线上,则m小于c.正确的个数是( )
,m)在此抛物线上,则m小于c.正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据抛物线的开口方向、对称轴的位置和与y轴的交点位置即可判断出a、b、c的符合,从而判断①;再根据方程![]() 的两根是-1和3,可求出点A坐标为(-1,0),点B坐标为(3,0),抛物线的对称轴为:直线x=
的两根是-1和3,可求出点A坐标为(-1,0),点B坐标为(3,0),抛物线的对称轴为:直线x=![]() ,从而求出抛物线上当x=1时,y<0,
,从而求出抛物线上当x=1时,y<0,
将x=1代入解析式即可判断a+b+c的符合,从而判断②;将x=-1和x=3分别代入方程![]() 中,用加减消元法消去b,即可判断③;根据抛物线的增减性即可判断④.
中,用加减消元法消去b,即可判断③;根据抛物线的增减性即可判断④.
解:∵抛物线的开口向上
∴a>0
∵对称轴在y轴右侧
∴a、b异号,即b<0
∵抛物线与y轴交于负半轴
∴c<0
∴abc>0,①正确;
∵方程![]() 的两根是-1和3
的两根是-1和3
∴点A坐标为(-1,0),点B坐标为(3,0),抛物线的对称轴为:直线x=![]()
∴横坐标为1,且在抛物线上的点位于AB之间
由图可知:抛物线上当x=1时,y<0
∴将x=1代入解析式中得y=a+b+c<0,②正确;
将x=-1和x=3分别代入方程![]() 中得
中得
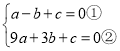
将①×3+②得:12a+4c=0
将等式两边同时除以4得:
3a+c=0,③正确;
由对称轴x=1可知:点C关于对称轴的对称点为(2,c)
而1<![]() <2
<2
故此时C关于对称轴的对称点,M(![]() ,m)都在对称轴的右侧
,m)都在对称轴的右侧
由图像可知:对称轴右侧y随x增大而增大
∴m<c,④正确;
故选D.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
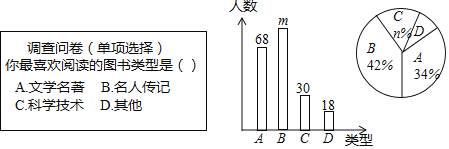
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年某县投入200万元用于农村“扶贫工程”,计划以后每年以相同的增长率投入,2018年该县计划投入“扶贫工程”338万元.
(1)求该县投入“扶贫工程”的年平均增长率.
(2)从2016年到2018年,该县三年共投入“扶贫工程”多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
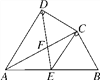
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)根据上述信息可知:甲命中环数的中位数是_____环,乙命中环数的众数是______环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
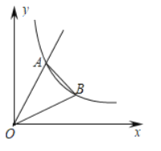
【题目】如图,正比例函数y1=k1x的图象与反比例函数y2=![]() (x>0)的图象相交于点A(
(x>0)的图象相交于点A(![]() ,2
,2![]() ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
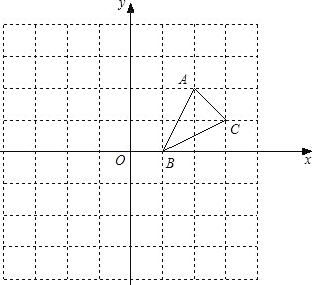
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com