解:(1)∵直线AB的解析式为y=2x+2,
∴点A、B的坐标分别为A(0,2)、B(-1,0);
又直线l的解析式为y=-3x+9,∴点C的坐标为(3,0).
由上,可设经过A、B、C三点的抛物线的解析式为y=a(x+1)(x-3),将点A的坐标代入,得:a=-

,
∴抛物线的解析式为y=-

x
2+

x+2,
∴抛物线的对称轴为x=1;
由于抛物线的开口向下,所以函数值随x的增大而增大时,x的取值范围是x≤1.
(2)过A作AE∥BC,交抛物线于点E;显然,点A、E关于直线x=1对称,
∴点E的坐标为E(2,2);
故梯形ABCE的面积为 S=

(2+4)×2=6.
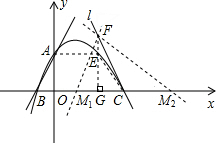
(3)假设存在符合条件的点H,作直线FH交x轴于M;
由题意知,S
△CFM=3,设F(m,n),易知m=2;
将F(2,n)的坐标代入y=-3x+9中,可求出n=3,则FG=3;
∴S
△CFM=

FG•CM=3,∴CM=2.
由C(3,0)知,M
1(1,0)、M
2(5,0),
设FM的解析式为y=kx+b:
由M
1(1,0)、F(2,3)得,FM
1解析式为y=3x-3,则FM
1与抛物线的交点H满足:

,
整理得,2x
2+5x-15=0,
∴x=
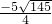
,
由M
2(5,0)、F(2,3)得,FM
2解析式为y=-x+5,则FM
2与抛物线的交点H满足:
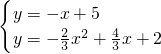
,整理得,2x
2-7x+9=0,
∵△<0,∴不符合题意,舍去;
即:H点的横坐标为
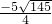
.
分析:(1)已知直线AB和直线l的解析式,易求得A、B、C三点的坐标,利用待定系数法即可求出抛物线的解析式;进而得出抛物线的对称轴方程,抛物线的开口向下,在对称轴左侧函数的函数值随x的增大而增大.
(2)四边形ABCE是梯形,且以BC为底,所以AE必与x轴平行,即A、E关于抛物线对称轴对称,由此能求得点E的坐标和AE的长,再根据梯形的面积公式求解即可.
(3)在(2)题中已求得了梯形ABCE的面积,则直线l、FH和x轴所围成的三角形的面积可得;将E点的横坐标代入直线l的解析式中即可求出F点的坐标,设FH与x轴的交点为M,以CM为底,点F的纵坐标的绝对值为高即可表达出△FMC的面积,再根据上面求得的面积具体值,即可求出CM的长由此得出点M的坐标;首先求出直线FM的解析式,联立抛物线的解析式即可得出H点的横坐标.
点评:此题主要考查了函数解析式的确定、函数增减性的判定、图形面积的解法等重要知识;最后一题中,要注意分情况讨论,以免漏解.

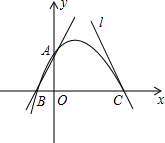 如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9 ?若存在,求点H的横坐标;若不存在,请说明理由.
?若存在,求点H的横坐标;若不存在,请说明理由. ,
, x2+
x2+ x+2,
x+2, (2+4)×2=6.
(2+4)×2=6.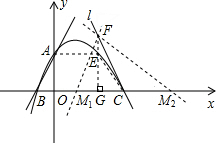 (3)假设存在符合条件的点H,作直线FH交x轴于M;
(3)假设存在符合条件的点H,作直线FH交x轴于M; FG•CM=3,∴CM=2.
FG•CM=3,∴CM=2. ,
,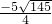 ,
,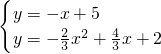 ,整理得,2x2-7x+9=0,
,整理得,2x2-7x+9=0,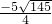 .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 如图,已知直线l1:y=
如图,已知直线l1:y=