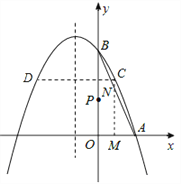
【题目】如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=﹣1．

（1）求抛物线对应的函数关系式；

（2）点P在y轴上，点M在x轴正方向上，过点M作x轴的垂线交抛物线于点C，OP=3OM．

①当四边形OMCP为矩形时，求OM的长；

②过点C作x轴的平行线，交抛物线于另一点D，求点P在直线CD的下方时，求CD的取值范围．

参考答案：

【答案】（1）抛物线的解析式为：y=－（x+1）2+4或；

（2）①当OM=时，四边形OMCP为矩形；

②点P在直线CD的下方时，CD的取值范围是2＜CD＜．

【解析】解：（1）根据题意，设抛物线的解析式为：y=a（x+1）2+k，

∵点A（1，0），B（0，3）在抛物线上，

∴，

解得：a=﹣1，k=4，

∴抛物线的解析式为：y=－（x+1）2+4或．

（2）①∵当四边形OMCP为矩形时，设OM= t，则OP=3 t，

则有OP=MC，即3t=－（t+1）2+4，

整理得：t2+5t﹣3=0，

解得t=，由于t=＜0，故舍去，

∴当OM=时，四边形OMCP为矩形；

②∵设OM= t时，函数y=－（t+1）2+4的对称轴为，

∴点C到直线的距离为t+1．

∴CD=2 t+2．

∵当OM=时，四边形OMCP为矩形，

此时OP=，点P在CD上，

∴点P在直线CD的下方时，t =OM＜．

∵CD=2 t+2，

∴CD＜

又∵点C与点B重合时, CD=2，点M在x轴正方向上，

∴求点P在直线CD的下方时，CD的取值范围是2＜CD＜．

关闭