
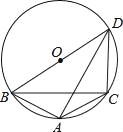
【题目】如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求弦DC的长.
【答案】![]()
【解析】
根据直径所对的圆周角是直角,可得∠BAD=∠BCD=90°;然后求出∠CAD=30°,利用同弧所对的圆周角相等,求出∠CBD=∠CAD=30°;根据圆内接四边形对角互补,求出∠BDC=60°;再根据等弦所对的圆周角相等,求出∠ADB=∠ADC,从而求出∠ADB=30°;解直角三角形求出BD;再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=![]() ×60°=30°,
×60°=30°,
在Rt△ABD中,AB=![]() AD=
AD=![]() ×6=2
×6=2![]() ,BD=2AB=4
,BD=2AB=4![]() ,
,
在Rt△BCD中,CD=![]() BD=2
BD=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AD上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC、BC上,则CE:CF=( )
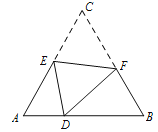
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
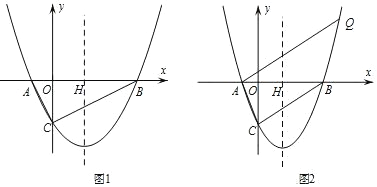
【题目】已知,抛物线 y=![]() x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=
x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=![]() 交 x 轴于点 H.
交 x 轴于点 H.
(1)若抛物线y=![]() x2+bx+c经过点(﹣4,6),求抛物线的解析式;
x2+bx+c经过点(﹣4,6),求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
(3)如图 2,过点A作AQ∥BC交抛物线于点Q,若点Q的纵坐标为﹣![]() c, 求点Q的坐标.
c, 求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.

(1)三角尺旋转了 度。
(2)连接CD,试判断△CBD的形状;
(3)求∠BDC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
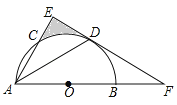
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内,如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°
∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.
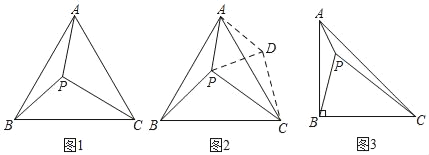
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
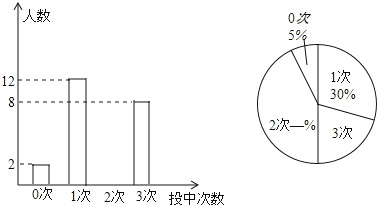
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com