
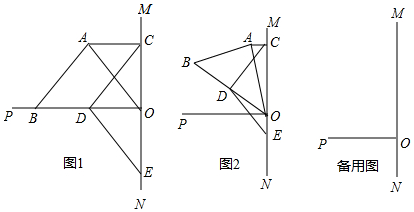
分析 (1)①如图1,证明AC=OC和OC=OE可得结论;
②根据勾股定理可得:AC2+CO2=CD2;
(2)如图2,(1)中的结论②不成立,作辅助线,构建全等三角形,证明A、D、O、C四点共圆,得∠ACD=∠AOB,同理得:∠EFO=∠EDO,再证明△ACO≌△EOF,得OE=AC,AO=EF,根据勾股定理得:AC2+OC2=FO2+OE2=EF2,由直角三角形中最长边为斜边可得结论;
(3)如图3,连接AD,则AD=OD证明△ACD≌△OED,根据△CDE是等腰直角三角形,得CE2=2CD2,等量代换可得结论(OC-OE)2=(OC-AC)2=2CD2,开方后是:OC-AC=$\sqrt{2}$CD.
解答 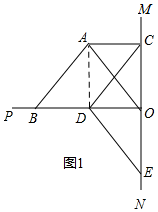 解:(1)①AC=OE,
解:(1)①AC=OE,
理由:如图1,∵在等腰Rt△ABO中,∠BAO=90°,
∴∠ABO=∠AOB=45°,
∵OP⊥MN,
∴∠COP=90°,
∴∠AOC=45°,
∵AC∥OP,
∴∠CAO=∠AOB=45°,∠ACO=∠POE=90°,
∴AC=OC,
连接AD,
∵BD=OD,
∴AD=OD,AD⊥OB,
∴AD∥OC,
∴四边形ADOC是正方形,
∴∠DCO=45°,
∴AC=OD,
∴∠DEO=45°,
∴CD=DE,
∴OC=OE,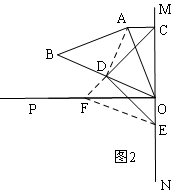
∴AC=OE;
②在Rt△CDO中,
∵CD2=OC2+OD2,
∴CD2=AC2+OC2;
故答案为:AC2+CO2=CD2;
(2)如图2,(1)中的结论②不成立,理由是:
连接AD,延长CD交OP于F,连接EF,
∵AB=AO,D为OB的中点,
∴AD⊥OB,
∴∠ADO=90°,
∵∠CDE=90°,
∴∠ADO=∠CDE,
∴∠ADO-∠CDO=∠CDE-∠CDO,
即∠ADC=∠EDO,
∵∠ADO=∠ACO=90°,
∴∠ADO+∠ACO=180°,
∴A、D、O、C四点共圆,
∴∠ACD=∠AOB,
同理得:∠EFO=∠EDO,
∴∠EFO=∠AOC,
∵△ABO是等腰直角三角形,
∴∠AOB=45°,
∴∠DCO=45°,
∴△COF和△CDE是等腰直角三角形,
∴OC=OF,
∵∠ACO=∠EOF=90°,
∴△ACO≌△EOF,
∴OE=AC,AO=EF,
∴AC2+OC2=FO2+OE2=EF2,
Rt△DEF中,EF>DE=DC,
∴AC2+OC2>DC2,
所以(1)中的结论②不成立;
(3)如图3,结论:OC-CA=$\sqrt{2}$CD,
理由是:连接AD,则AD=OD,
同理:∠ADC=∠EDO,
∵∠CAB+∠CAO=∠CAO+∠AOC=90°,
∴∠CAB=∠AOC,
∵∠DAB=∠AOD=45°,
∴∠DAB-∠CAB=∠AOD-∠AOC,
即∠DAC=∠DOE,
∴△ACD≌△OED,
∴AC=OE,CD=DE,
∴△CDE是等腰直角三角形,
∴CE2=2CD2,
∴(OC-OE)2=(OC-AC)2=2CD2,
∴OC-AC=$\sqrt{2}$CD,
故答案为:OC-AC=$\sqrt{2}$CD.
点评 本题是几何变换的综合题,考查了三角形全等的性质和判定、等腰直角三角形的性质和判定、旋转的性质、勾股定理、四点共圆的性质等知识,并运用了类比的思想解决问题,有难度,尤其是第二问,结论不成立,要注意辅助线的作法;本题的2、3问能标准作图是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
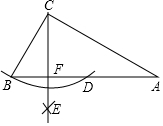 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
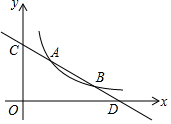 直线y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
直线y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则△ADE的周长为( )
如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则△ADE的周长为( )| A. | 8 | B. | 3 | C. | 9 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测).无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测).无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com